Hai vòi nước cùng cháy vào một bể thì sau 1 giờ 52 phút đầy bể. Người ta mở vòi một trong hai giờ thì khoá lại và mở tiếp vòi hai thì sau 1 giờ 45 phút nữa mới đầy bể. Hỏi nếu mở riêng từng vòi thì bao lâu sẽ đầy bể?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 10 2023
Gọi thời gian chảy riêng một mình đầy bể của vòi 1 và vòi 2 lần lượt là a(giờ) và b(giờ)(ĐK: a>0 và b>0)
Trong 1h, vòi 1 chảy được \(\dfrac{1}{a}\)(bể)
Trong 1h, vòi 2 chảy được \(\dfrac{1}{b}\left(bể\right)\)
Trong 1h, hai vòi chảy được: \(\dfrac{1}{3}\left(bể\right)\)
Do đó, ta có: \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{3}\left(1\right)\)
Trong 30p thì vòi 1 chảy được: \(\dfrac{1}{2}\cdot\dfrac{1}{a}\left(bể\right)\)
Trong 10h30p thì vòi 2 chảy được \(\dfrac{1}{10,5}\cdot\dfrac{1}{b}=\dfrac{2}{21}\cdot\dfrac{1}{b}\left(bể\right)\)
Theo đề, ta có: \(\dfrac{1}{2}\cdot\dfrac{1}{a}+\dfrac{2}{21}\cdot\dfrac{1}{b}=1\)(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{2}\cdot\dfrac{1}{a}+\dfrac{2}{21}\cdot\dfrac{1}{b}=1\\\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{2}\cdot\dfrac{1}{a}+\dfrac{2}{21}\cdot\dfrac{1}{b}=1\\\dfrac{1}{2}\cdot\dfrac{1}{a}+\dfrac{1}{2}\cdot\dfrac{1}{b}=\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{17}{42}b=\dfrac{5}{6}\\\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=-\dfrac{35}{17}\left(loại\right)\\a=\dfrac{122}{51}\end{matrix}\right.\)
=>Đề sai rồi bạn
10 tháng 7 2023
Gọi thời gian chảy một mình đầy bể của vòi 1 và vòi 2 lần lượt là a,b
Theo đề, ta có hệ:
1/a+1/b=1/1,5 và 1/4*1/a+1/3*1/b=1/5
=>a=15/4 và b=5/2
BT
15 tháng 7 2017
Đổi: 30'=0,5 giờ
Sau 0,5h thì 2 vòi chảy được số phần bể là: \(\frac{0,5}{3}=\frac{1}{6}\)(bể)
Số phần bể còn lại là: \(1-\frac{1}{6}=\frac{5}{6}\)(bể)
Như vậy sau 10 giờ thì vòi 2 chảy được 5/6 bể
=> Thời gian để vòi 2 chảy đầy bể là: \(\frac{10x6}{5}=12\left(giờ\right)\)
=> Sau 3 giờ thì vòi 2 chảy được số phần bể là: \(\frac{3}{12}=\frac{1}{4}\left(bể\right)\)
=> Sau 3 giờ thì vòi 1 chảy được số phần bể là: \(1-\frac{1}{4}=\frac{3}{4}\left(bể\right)\)
=> Thời gian để vòi 1 chảy đầy bể là: \(\frac{3x4}{3}=4\left(giờ\right)\)
Đáp số: Vòi 1=4 giờ; Vòi 2=12 giờ
CM
1 tháng 2 2018
Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là x (giờ), (x > 0)
Trong một giờ:
- Vòi thứ nhất chảy được 1/x (bể)
- Vòi thứ hai chảy được 1/(x+4) (bể)
- Vòi thứ ba chảy được 1/6 (bể)
Khi mở cả ba vòi thì vòi thứ nhất và vòi thứ hai chảy vào bể còn vòi thứ ba cho nước ở bể chảy ra nên ta có phương trình:
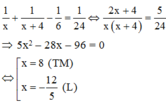
Vậy chỉ dùng vòi thứ nhất thì sau 8 giờ bể đầy nước
Đáp án: D
Bài giải
Hai vòi nước cùng chảy vào một bể thì sau 1 giờ 52 phút đầy bể.
=> Vòi một chảy 1 giờ 52 phút + Vòi hai chảy 1 giờ 52 phút thì đầy bể.( Ta gọi đây là lần 1)
Mở vòi một trong hai giờ thì khoá lại và mở tiếp vòi hai thì sau 1 giờ 45 phút nữa mới đầy bể.
=> Vòi một chảy 2 giờ + Vòi hai chảy 1 giờ 45 phút thì đầy bể. (Ta gọi đây là lần 2)
Ta so sánh lần 1 với lần 2:
Vòi 1: Chảy nhiều hơn: 2 giờ - 1 giờ 52 phút = 8 phút
Vòi 2: Chảy ít hơn: 1 giờ 52 phút - 1 giờ 45 phút = 7 phút
Vậy lượng nước vòi một chảy trong 8 phút bằng lượng nước vòi 2 chảy trong 7 phút.
Vòi một chảy trong 2 giờ(ở lần 2) và phải chảy thêm lượng nước mà vòi hai chảy trong 1 giờ 45 phút hết:
1 giờ 45 phút : 7 x 8 = 120 (phút)
Đổi 120 phút = 2 giờ
Vậy thời gian vòi một chảy riêng đầy bể là: 2 giờ + 2 giờ = 4 giờ
Vòi hai chảy trong 1 giờ 45 phút(ở lần 2) và phải chảy thêm lượng nước mà vòi một chảy trong 2 giờ hết:
2 giờ : 8 x 7 = 105 (phút)
Đổi 105 phút = 1 giờ 45 phút
Vậy thời gian vòi hai chảy riêng đầy bể là: 1 giờ 45 phút + 1 giờ 45 phút = 3 giờ 30 phút
Đ/s : Vòi một: 4 giờ ; Vòi hai: 3 giờ 30 phút
Bài toán này khó thật, mình giải mãi mới ra. Rất vui vì giúp được bạn. Vì mình giải dài quá nên hơi rối, những chỗ quân trọng mình tô đen nhé.