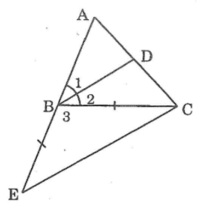
Cho tam giác ABC , tia phân giác của góc B cắt AC tại D. Trên tia đối của tia BA lấy điểm E: BE = BC . C/m: BD // EC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 1 2016
\(\Delta EBCcó:BE=BC\left(gt\right)\)
\(\Rightarrow\Delta EBC\) cân tại B
\(\Rightarrow\) góc E = góc C
Ta có : góc ABD + góc DBC + góc CBE = 1800 (kề bù)
\(\Rightarrow\) góc CBE = 1800 - ( góc ABD + góc DBC)
Và ta lại có: góc E + góc CBE + góc C = 1800 (tổng 3 góc trong tam giác EBC)
\(\Rightarrow\) góc CBE = 1800 - ( góc E + góc C)
Mà : góc ABD = góc DBC ( vì BD là tia phân giác của góc ABC)
góc E = C ( cmt )
\(\Rightarrow\) góc DBC = góc C
Mà : 2 góc này nằm ở vị trí so le trong
\(\Rightarrow BDsong^2EC\)
16 tháng 6 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
BA=BE
=>ΔBAD=ΔBED
=>góc ABD=góc EBD
=>BD là phân giác của góc ABE
b: BA=BE
DA=DE
=>BD là trung trực của AE
CM
26 tháng 10 2019
Ta có: BD là tia phân giác của ∠ABC (giả thiết)
Suy ra: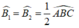 
(1)
Lại có: BE = BC (giả thiết)
=>∆BEC cân tại B (theo định nghĩa)
Suy ra: ∠E= ∠BCE (tính chất tam giác cân)
∆BEC có ABC là góc ngoài đỉnh B
=>∠ABC= ∠E + ∠BCE (tính chất góc ngoài tam giác)
Suy ra: ∠ABC=2∠E
Hay ∠E = (1/2)∠ABC (2)
Từ (1) và (2) suy ra: ∠E = ∠B1 = (1/2)∠ABC
Vậy BD // CE (vì có cặp góc ở vị trí đồng vị bằng nhau)
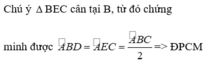
Ta có : BE = BC ( gt)
=> ∆BEC cân tại B
=> E = BCE
Mà ta thấy ABC = E + BCE ( góc ngoài ∆ bằng tổng 2 góc trong ko kề với nó)
Mà E = BCE ( cmt)
=> ABC = 2E
Mà ABD = DBC ( BD là phân giác ABC )
=> E = BCE = ABD = DBC
=> DBC = BCE
Mà 2 góc này ở vị trí so le trong
=> BD //EC ( dpcm)