Hai cầu thủ Tiến Dũng và Văn Lâm đứng ở hai cầu môn của một sân bóng đá (Tiến Dũng ở vị trí A và Văn Lâm ở vị trí B trong hình vẽ, lúc đầu 2 người đứng cách nhau nửa vòng sân). Hai người cùng xuất phát chạy theo đường biên của sân vận động và ngược chiều nhau với vận tốc không đổi (Tiến Dũng chạy cùng chiều kim đồng hồ). Lần đầu tiên hai người gặp nhau tại một điểm C cách vị trí A 83m (quãng đường AC) và họ tiếp tục chạy cho đến khi gặp nhau lần thứ 2 tại một điểm D cách vị trí B 76m (quãng đường BD). Tìm chu vi của sân vận động.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ABC}+59^0+82^0=180^0\)
=>\(\widehat{ABC}=39^0\)
Xét ΔABC có \(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{25}{sin39}=\dfrac{AB}{sin82}\)
=>\(AB=25\cdot\dfrac{sin82}{sin39}\simeq39,34\left(m\right)\)

Trong tam giác BCD, góc DCB là góc tù nên là góc lớn nhất. Cạnh DB đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DB > DC (1)
Vì góc DBA là góc ngoài tại đỉnh B của tam giác BCD nên \(\widehat {ABD} > \widehat {BCD}\)nên góc DBA cũng là góc tù.
Trong tam giác ABD, góc DCA là góc tù nên là góc lớn nhất. Cạnh DA đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DA > DB (2)
Từ (1) và (2) \( \Rightarrow \) DA > DB > DC
Vậy DA dài nhất, DC ngắn nhất
Do đó, cầu thủ C gần trái bóng nhất, cầu thủ A xa trái bóng nhất.

gia su 11 cau thu la 11 diem
chon 1 diem noi voi 10 diem con lai ta duoc 10 duong thang
co tat ca 11 diem nen so duong thang la: 11.10 (duong thang)
nhung nhu vay moi duong thang duoc tinh hai lan, nen so duong thang thuc su co la: (11.10):2=55 (duong thang)

Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P A = 1 8 + 1 16 = 3 16 .

Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P ( A ) = 1 8 + 1 16 = 3 16 .

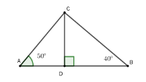
Độ cao của diều là CD, độ dài AB = 100m. Trung đứng ở A, Dũng đứng ở B
Gọi AD = x (0 < x < 100)
=> BD = 100 – x
Xét ACD vuông tại D, ta có CD = AD.tan A = x . tan 50 0
Xét ABD vuông tại D, ta có CD = BD.tan B = (100 – x). tan 40 0
Nên x . tan 50 0 = (100 – x). tan 40 0
![]()
Vậy độ cao của diều lúc đó so với mặt đất là 49,24m
Đáp án cần chọn là: B


Gọi \(v_A\)là vận tốc Tiến Dũng
Gọi \(v_B\)là vận tốc Văn Lâm
và x là chu vi sân =>AB=x/2
Chặn 1: Gặp tại C: \(\frac{83}{v_A}=\frac{\frac{x}{2}-83}{v_B}=\frac{1}{2}\cdot\frac{x}{v_A+v_B}\)
Chặn 2: Gặp tại D: \(\frac{S_{CD\left(A\right)}}{v_A}=\frac{S_{CD\left(B\right)}}{v_B}\Rightarrow\frac{BC+BD}{v_A}=\frac{AC+AD}{v_B}\Rightarrow\frac{\frac{x}{2}-83+76}{v_A}=\frac{\frac{x}{2}+83-76}{v_B}=\frac{x}{v_A+v_B}\)
Từ đây liên hệ đc đại lương 2 chặn
Giải đc: x=346 m
Đặt chu vi sân vận động là \(x.\)
Vì hai người chạy với vận tốc không đổi nên:
Tỉ số quãng đường chạy được sau lần đầu gặp nhau của Tiến Dũng và Văn Lâm: \(\frac{83}{\frac{1}{2}x-83}\)
Tỉ số quãng đường chạy được sau lần thứ hai gặp nhau của Tiến Dũng và Văn Lâm: \(\frac{\left(\frac{1}{2}x-83\right)+76}{83+\left(\frac{1}{2}x-76\right)}=\frac{\frac{1}{2}x-7}{\frac{1}{2}x+7}\)
\(\Rightarrow\frac{83}{\frac{1}{2}x-83}=\frac{\frac{1}{2}x-7}{\frac{1}{2}x+7}\)
\(\Rightarrow83\left(\frac{1}{2}x+7\right)=\left(\frac{1}{2}x-83\right)\left(\frac{1}{2}x-7\right)\)
\(\Rightarrow83\frac{1}{2}x+83\cdot7=\frac{\left(x-83\cdot2\right)}{2}\cdot\frac{\left(x-7\cdot2\right)}{2}\)
\(\Rightarrow41.5x+581=\frac{\left(x-166\right)\left(x-14\right)}{4}\)
\(\Rightarrow4\left(41.5x+581\right)=\left(x-166\right)\left(x-14\right)\)
\(\Rightarrow4\cdot41.5x+4\cdot581=-166x+x^2-14x+14\cdot166\)
\(\Rightarrow166x+2324=\left(-166x-14x\right)+x^2+2324\)
\(\Rightarrow166x=-180x+x^2\)
\(\Rightarrow x^2=166x+180x\)
\(\Rightarrow x^2=346x\)
\(\Rightarrow x=346\)
Mình làm vậy đúng không nhỉ?