Trong tất cả nghiệm (x,y) của phương trình : 2x + 3y = 1 . Hãy chỉ ra nghiệm có tổng 3x2 + 2y2 có nghiệm nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 10 2016
1/ Đề đúng phải là \(3x^2+2y^2\) có giá trị nhỏ nhất nhé.
Áp dụng BĐT BCS , ta có
\(1=\left(\sqrt{2}.\sqrt{2}x+\sqrt{3}.\sqrt{3}y\right)^2\le\left[\left(\sqrt{2}\right)^2+\left(\sqrt{3}\right)^2\right]\left(2x^2+3y^2\right)\)
\(\Rightarrow2x^2+3y^2\ge\frac{1}{5}\). Dấu "=" xảy ra khi \(\begin{cases}\frac{\sqrt{2}x}{\sqrt{2}}=\frac{\sqrt{3}y}{\sqrt{3}}\\2x+3y=1\end{cases}\) \(\Leftrightarrow x=y=\frac{1}{5}\)
Vậy \(3x^2+2y^2\) có giá trị nhỏ nhất bằng 1/5 khi x = y = 1/5
30 tháng 10 2016
2/ Áp dụng bđt AM-GM dạng mẫu số ta được
\(6=\frac{\left(\sqrt{2}\right)^2}{x}+\frac{\left(\sqrt{3}\right)^2}{y}\ge\frac{\left(\sqrt{2}+\sqrt{3}\right)^2}{x+y}\)
\(\Rightarrow x+y\ge\frac{\left(\sqrt{2}+\sqrt{3}\right)^2}{6}\)
Dấu "=" xảy ra khi \(\begin{cases}\frac{\sqrt{2}}{x}=\frac{\sqrt{3}}{y}\\\frac{2}{x}+\frac{3}{y}=6\end{cases}\) \(\Rightarrow\begin{cases}x=\frac{2+\sqrt{6}}{6}\\y=\frac{3+\sqrt{6}}{6}\end{cases}\)
Vậy ......................................
CM
25 tháng 3 2018
Ta có
2 x + 3 y = 7 2 − m 4 x − y = 5 m ⇔ 4 x + 6 y = 7 − 2 m 4 x − y = 5 m ⇔ 7 y = 7 − 7 m 4 x − y = 5 m ⇔ y = 1 − m 4 x − 1 − m = 5 m ⇔ y = 1 − m x = 4 m + 1 4
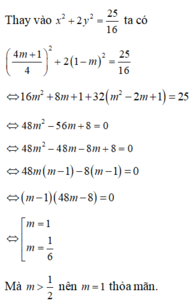
Đáp án: B
CM
11 tháng 1 2017
Đáp án A
Em có x 3 − 3 x 2 − m = 0 ⇔ x 3 − 3 x 2 = m
Khi đó yêu cầu đầu bài tương đương với đồ thị hàm số y = x 3 − 3 x 2 cắt đường thẳng y = m tại 3 điểm trong đó có 2 điểm có hoành độ lớn hơn 1. Em có đồ thị hàm số y = x 3 − 3 x 2 như hình bên.
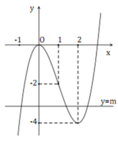
Từ đồ thị em thấy − 4 < m < − 2
CM
1 tháng 7 2018
Phương trình có hai nghiệm phân biệt ⇔ ∆ > 0
⇔ m 2 - 8 m + 16 = 0 m - 4 2 > 0 ⇔ m ≠ 4 *
Theo định lí Viet, ta có:
x 1 . x 2 = m − 1 3 ; x 1 + x 2 = m + 2 3 x 1 = 2 x 2 ⇔ x 1 = 2 9 ( m + 2 ) , x 2 = 1 9 ( m + 2 ) x 1 . x 2 = m − 1 3
⇒ 2 81 ( m + 2 ) 2 = m − 1 3 ⇔ 2 m 2 − 19 m + 35 = 0 ⇔ m = 5 2 m = 7 (thỏa mãn (*))
Đáp án cần chọn là: A
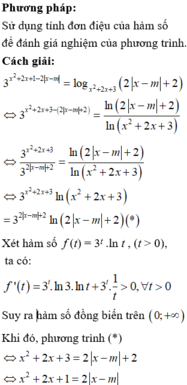
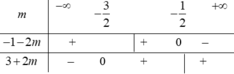
Ta có : \(1=\left(2\text{x}+3y\right)^2=\left(\frac{2}{\sqrt{3}}\cdot x\cdot\sqrt{3}+\frac{2}{\sqrt{2}}\cdot y\cdot\sqrt{2}\right)^2\) \(\le\left(\frac{4}{3}+\frac{9}{2}\right)\left(3\text{x}^2+2y^2\right)=\frac{35}{6}\left(3\text{x}^2+2y^2\right)\Rightarrow3\text{x}^2+2y^2\ge\frac{6}{35}\)
Dấu "=" xảy ra khi ta có :
\(\text{x}\sqrt{3}\div\frac{2}{\sqrt{3}}=y\sqrt{2}\div\frac{3}{\sqrt{2}}\Leftrightarrow\hept{\begin{cases}2\text{x}+3y=1\\\frac{3\text{x}}{2}=\frac{2y}{3}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{4}{35}\\y=\frac{9}{35}\end{cases}}\)
Vậy \(\left(3\text{x}^2+2y^2\right)_{\text{Min}}=\frac{6}{35}\)đạt được khi \(x=\frac{4}{35}\)và \(y=\frac{9}{35}\)