Tìm hai số hữu tỉ x và y sao cho x - y = x.y = x : y (y ≠ 0).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: x – y = x.y ⇒ x = x.y + y = y.(x + 1) (1)
Suy ra: x : y = y.(x + 1) : y = x + 1 (2)
Theo giả thiết, x : y = x – y nên từ (2) suy ra:
⇒ x – y = x + 1 ⇒ y = −1
Thay y = - 1 vào (1) ta được:
x = (-1)(x + 1) ⇒ x = − x – 1 ⇒ 2x = −1 ⇒ x = (-1)/2
Vậy x = −1/2; y = −1.

Vì xy = x : y suy ra y^2 = 1 ---> y = 1 hoặc y = -1
+ Nếu y = 1 ---> x - 1 = x.1 (vô nghiệm nên tr/hợp này loại)
+ Nếu y = -1 ---> x + 1 = - x ---> 2x = -1 ---> x = -1/2 (nhận)
Vậy x = -1/2 ; y = -1.
l.anh êi , mở bài 21 trang 11 trong vở bài tập có bài này đấy

Lời giải:
$x$ là số hữu tỉ khác $0$. Đặt $x=\frac{a}{b}$ với $a,b$ là số nguyên, $b\neq 0$.
Giả sử $x+y$ là số hữu tỉ. Đặt $x+y=\frac{c}{d}$ với $c,d\in\mathbb{Z}, d\neq 0$
$\Rightarrow y=\frac{c}{d}-x=\frac{c}{d}-\frac{a}{b}=\frac{bc-ad}{bd}$ là số hữu tỉ (do $bc-ad, bd\in\mathbb{Z}, bd\neq 0$)
Điều này vô lý do $y$ là số vô tỉ.
$\Rightarrow$ điều giả sử là sai. Tức là $x+y$ vô tỉ.
Hoàn toàn tương tự, $x-y$ cũng là số vô tỉ.
-------------------------------
Chứng minh $xy$ vô tỉ.
Giả sử $xy$ hữu tỉ. Đặt $xy=\frac{c}{d}$ với $c,d$ nguyên và $d\neq 0$
$\Rightarrow y=\frac{c}{d}:x=\frac{c}{d}:\frac{a}{b}=\frac{bc}{ad}\in\mathbb{Q}$
Điều này vô lý do $y\not\in Q$
$\Rightarrow$ điều giả sử là sai $\Rightarrow xy$ vô tỉ.
-------------------------------
CM $\frac{x}{y}$ vô tỉ.
Giả sử $\frac{x}{y}$ hữu tỉ. Đặt $\frac{x}{y}=\frac{c}{d}$ với $c,d$ nguyên, $d\neq 0$
$\Rightarrow y=x:\frac{c}{d}=\frac{a}{b}: \frac{c}{d}=\frac{ad}{bc}\in\mathbb{Q}$
Điều này vô lý do $y\not\in Q$
$\Rightarrow$ điều giả sử là sai. Tức là $\frac{x}{y}$ vô tỉ.

xy = x/y
<=> xy² = x
<=> y² = 1
<=> y = 1 hoặc y = -1
-nếu y = 1 có
x + 1 = x
<=> 1 = 0 (loại)
-nếu y = -1 có
x - 1 = -x
<=> x = 1/2
thay vào thấy thỏa mãn
vậy x = 1/2 ; y = -1
xy = x/y
<=> xy² = x
<=> y² = 1
<=> y = 1 hoặc y = -1
-nếu y = 1 có
x + 1 = x
<=> 1 = 0 (loại)
-nếu y = -1 có
x - 1 = -x
<=> x = 1/2
thay vào thấy thỏa mãn
vậy x = 1/2 ; y = -1

a. Theo t/c dãy tỉ số = nhau:
\(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{42}{7}=6\)
=>\(\frac{x}{2}=6\Rightarrow x=6.2=12\)
=>\(\frac{y}{5}=6\Rightarrow y=6.5=30\)
Vậy x=12; y=30.
b. \(\left|x-0,25\right|-\frac{5}{6}=1\frac{2}{3}\)
=> \(\left|x-0,25\right|=1\frac{2}{3}+\frac{5}{6}\)
=> \(\left|x-0,25\right|=\frac{5}{2}=2,5\)
+) x-0,25=2,5
=> x=2,5+0,25
=> x=2,75
+) x-0,25=-2,5
=> x=-2,5+0,25
=> x=-2,25
Vậy x \(\in\){-2,25; 2,75}.
c. y=kx
=> -17=k.8
=> k=-17/8
Vậy hệ số tỉ lệ là -17/8.
a) \(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{42}{7}=6\)
=> x=12 ; y = 30
b) \(\left|x-0,25\right|-\frac{5}{6}=1\frac{2}{3}=>\left|x-0,25\right|=\frac{5}{3}+\frac{5}{6}=\frac{5}{2}=2,5\)
=> x-0,25 = 2,5 hoac: -2,5
=> x = 2,75 hoac x= -2,25
Vay: x la { 2,75 ; -2,25 }
c) Ti le gi vay ban.
Neu thuan thi he so ti le la: \(-\frac{17}{8}\)
Neu nghich thi he so ti le la : -136


Cộng theo từng vế các đẳng thức đã cho, ta được:
x.(x + y + z) + y(x + y + z) + z.(x+ y + z) = - 5 + 9 + 5
⇔ (x + y + z). (x + y + z ) = 9
Suy ra: (x + y + z)2 = 9 ⇒ x + y + z = ±3
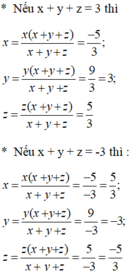
\(x-y=x.y\Rightarrow x=x.y+y=y\left(x+1\right)\)
\(x:y=y.\left(x+1\right):y=x+1\)
\(\Rightarrow x-y=x+1\Rightarrow y=-1\)
\(x=\left(-1\right)\left(x+1\right)\Rightarrow x=-x-1\)
\(\Rightarrow2x=-1\Rightarrow x=-\frac{1}{2}\)
Vậy \(x=-\frac{1}{2};y=-1\)
\(x-y=xy=\frac{x}{y}\left(y\ne0\right)\)
\(\Rightarrow x-y=xy\Rightarrow x=xy+y=\left(x+1\right)y\)
Thay vào ta có:\(x-y=\frac{x}{y}=\frac{\left(x+1\right)y}{y}=x+1\Rightarrow x-y=x+1\Rightarrow-y=1\Rightarrow y=-1\)
mà\(x=xy+y\Rightarrow x=x\left(-1\right)+\left(-1\right)=-x-1\)
\(\Rightarrow x=-x-1\Rightarrow2x=-1\Rightarrow x=\frac{-1}{2}\)
Vậy\(x=\frac{-1}{2},y=-1\)