Tìm số tự nhiên n nhỏ nhất thỏa đồng thời 2 điều kiện sau:
a) n là bội của 3 và 4
b) các chữ số của số đó chỉ có thể là 4, 6 (mỗi số xuất hiện ít nhất một lần).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 6 2017
Gọi 
là số cần lập a1 + a2 + a3 = 10
Theo bài ra ta có: 
(1)
Mà 
và đôi một khác nhau nên
a1,a2,a3,a4,a5,a6 = 1 + 2 + 3 + 4 + 5 + 6 =21
(2)
Từ (1), (2) suy ra: a1 + a2 + a3 = 10
Phương trình này có các bộ nghiệm là: ( a1 , a2 , a3 ) = (1,3,6); (1,4,5); (2,3,5)
Với mỗi bộ ta có 3!.3!=36 số.
Vậy có cả 3.36=108 số cần lập.
Chọn C.
CM
20 tháng 10 2017
Chọn đáp án C
Cách 1: Gọi x = a 1 a 2 . . . a 6 ¯ , a i ∈ 1 , 2 , 3 , 4 , 5 , 6 là số cần lập
Theo bài ra ta có:
Mà a 1 , a 2 , a 3 , a 4 , a 5 , a 6 ∈ 1 , 2 , 3 , 4 , 5 , 6 và đôi một khác nhau nên
Từ (1), (2) suy ra: a 1 + a 2 + a 3 = 10
Phương trình này có các bộ nghiệm là:
Với mỗi bộ ta có 36 số.
Vậy có cả thảy 3.36=108 số cần lập.
Cách 2: Gọi x = a b c d e f là số cần lập
Ta có:
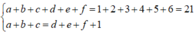
⇒ a + b + c = 11 .
Do a , b , c ∈ 1 , 2 , 3 , 4 , 5 , 6
Suy ra ta có các cặp sau:
Với mỗi bộ như vậy ta có 3! cách chọn a, b, c và 3! cách chọn d ,e ,f
Do đó: 3!.3!.3!= 108 số thỏa yêu cầu bài toán
15 tháng 11 2015
1)100008
2)1026
3)(n+2)(n+2)(n+2)+2 chia hết cho n+2
-Vì 3(n+2) chia hết cho n+2 nên 2 cũng chia hết cho n+2
Vậy n+2 là ước của 2 ; U(2)={1;2}
=>n+2=2
=> n=0
4)(x+5) chia hết cho 5 => x chia hết cho 5
(x-12) chia hết cho 6=> x chia hết cho 6
(x+14) chia hết cho 7=> x chia hết cho 7
số nhỏ nhất khác 0 chia hết cho 5;6;7 là :210
5)Nếu số đó chia hết cho cả 3 và 4 thì số đó chia hết cho 12
=> số đó là bội của 12 trong khoảng 100 đến 200
số đó \(\in\){108;120;132;144;156;168;;180;192}
Có 8 số
6)645
7)Nếu cạnh của hình Lập Phương = 2 (cm) thì thể tích ban đầu của nó là :2.2.2=8(\(cm^3\))
Độ dài của cạnh hình lập phương mới là :40(cm) thể tích của nó là :40.40.40=64000(\(cm^3\))
Thể tich của nó gấp :64000:8=8000 lần thể tích ban đầu
8)102345
17 tháng 5 2016
Ta có 1+2+3+4+5+6+ =21 Vậy tổng của 3 chữ số đầu là 10
Dễ thấy 1+3+6 = 1+4+5 = 2+3+5
Vậy có 3 cách chọn 3 nhóm 3 chữ số đầu (1,3,6 hoặc 1,4,5 hoặc 2,3,5)
Với 1 cách chọn nhóm 3 chữ số thì có 3! cách để lập ra số \(\overline{a_1a_2a_3}\)
Với 3 số còn lại thì có 3! cách để lập ra số \(\overline{a_4a_5a_6}\)
(ở đây \(\overline{a_1a_2a_3a_4a_5a_6}\) là số thỏa mãn yêu cầu đề ra)
Theo quy tắc nhân ta có 3.6.6 = 108
Vậy có 108 số cần tìm
TN
16 tháng 5 2020
Em thấy như này còn thiều trường hợp hay sao ý ạ tại ba số nhỏ hơn đâu nhất thiết phải bằng 10 ạ 123 vs 345 vẫn tỏa mãn đấy chứ ạ.Có thể cho em là mình sai ở đâu hay kế quả thế nào được không ạ??
#)Giải :
Vì bội chung của 3 và 4 chia hết cho 3 và 4 => số đó chia hết cho 12
=> Ta tìm được : \(B\left(12\right)=\left\{12;24;36;48;60;72;84;96;108;...\right\}\)
Rùi tự xét típ nha ^^
Ta có:
\(n\in BC\left(3,4\right)\Rightarrow n⋮3,4\)
Vì \(n⋮4\) nên 2 chữ số tận cùng của n phải chia hết cho 4 (dấu hiệu chia hết cho 4) mà các chữ số của n chỉ có thể là 4 hoặc 6\(\Rightarrow\)2 chữ số tận cùng của n là 44 hoặc 64
TH1: 2 chữ số tận cùng của là 44
Vì \(n⋮3\Rightarrow\) tổng các chữ số của n phải chia hết cho 3
Vì các chữ số của n chỉ có thể là 4 hoặc 6\(\Rightarrow\)các số đó là 4644 và 6444 (do có cả số 4 và 6 và \(4+6+4+4,6+4+4+4⋮3\))
Mà đề yêu cầu là tìm số nhỏ nhất\(\Rightarrow\)số đó là 4644
TH2: 2 chữ số tận cùng của là 64
Vì \(n⋮3\Rightarrow\) tổng các chữ số của n phải chia hết cho 3
Vì các chữ số của n chỉ có thể là 4 hoặc 6\(\Rightarrow\)số đó là 4464 (do có cả số 4 và 6 và \(4+4+6+4⋮3\))
Mà \(4464\left(TH2\right)< 4644\left(TH1\right)\Rightarrow\)số đó là 4464 (do đề yêu cầu tìm số nhỏ nhất)