Giải hộ bài này vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm

Bạn nên gõ hẳn câu bạn muốn trợ giúp. Nếu không, hãy chụp đề một cách rõ ràng. Không chụp quá nhiều bài trong 1 post nhé. Như vậy khả năng nhận được trợ giúp của bạn sẽ cao hơn.

Gọi x (m) là chiều rộng bạn đầu của khu vườn hình chữ nhật (x>0)
Chiều dài ban đầu của khu vườn hcn là: x + 3 (m)
Chiều rộng lúc sau của khu vườn hcn là: x + 2 (m)
Chiều dài lúc sau của khu vườn hcn là: x + 3 - 4 = x - 1 (m)
Diện tích ban đầu của khu vườn hcn là: x(x + 3) (m^2)
Diện tích lúc sau của khu vườn hcn là: (x + 2)(x - 1) (m^2)
Theo đề bài ta có phương trình:
x(x+3) - (x + 2)( x - 1) = 50
\(x^2\) + 3x - (\(x^2\) - x + 2x -2) = 50
\(x^2\) + 3x - \(x^2\) + x - 2x + 2 = 50
2x = 50 - 2
2x = 48
x = 24 (Nhận) (m)
Vậy chiều rộng ban đầu của khu vườn hcn là 24m
chiều dài ban đầu của khu vườn hcn là 24 + 3 = 27m

b, PTGD (d1) và trục hoành là \(2x+5=0\Leftrightarrow x=-\dfrac{5}{2}\Leftrightarrow B\left(-\dfrac{5}{2};0\right)\Leftrightarrow OB=\dfrac{5}{2}\)
PTGD (d2) và trục hoành là \(2-x=0\Leftrightarrow x=2\Leftrightarrow A\left(2;0\right)\Leftrightarrow OA=2\)
Do đó \(AB=OA+OB=\dfrac{9}{2}\)
PTHDGD (d1) và (d2) là \(2x+5=2-x\Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow C\left(-1;3\right)\)
Gọi H là chân đg cao từ C tới Ox thì \(CH=3\)
Do đó \(S_{ABC}=\dfrac{1}{2}CH\cdot AB=\dfrac{1}{2}\cdot\dfrac{9}{2}\cdot3=\dfrac{27}{4}\left(đvdt\right)\)
c, Vì \(-1=-1;2\ne4\) nên (d2)//(d3)

f: =-1/8-7/6+3/4-1
=-3/24-28/24+18/24-1
=-31/24+18/24-1
=-13/24-1=-37/24
g: \(=6\cdot\dfrac{-8}{27}-3\cdot\dfrac{4}{9}+\dfrac{4}{3}+4\)
=-48/27+4
=108/27-48/27
=60/27
=20/9
h: \(=\left[6\cdot\dfrac{1}{9}+1+1\right]\cdot\left(-3\right)-1\)
=(2/3+2)*(-3)-1
=-2-6-1
=-3-6=-9

Bạn có thể đăng lại rồi chia nhỏ câu hỏi ra được không ạ? nếu có thể thì đăng full toàn bộ văn bản lên nữa để làm được câu 4

\(ĐK:x\ge5\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x}=a\\\sqrt{x-5}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow4b^2-3a^2=x-20\)
\(PT\Leftrightarrow4b^2-3a^2+a+b+ab=0\\ \Leftrightarrow4ab+4b^2-3a^2-3ab+a+b=0\\ \Leftrightarrow4b\left(a+b\right)-3a\left(a+b\right)+\left(a+b\right)=0\\ \Leftrightarrow\left(a+b\right)\left(4b-3a+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a+b=0\left(\text{loại do }a+b>0\right)\\4b-3a+1=0\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow4\sqrt{x-5}=3\sqrt{x}-1\\ \Leftrightarrow16x-80=9x-6\sqrt{x}+1\\ \Leftrightarrow7x+6\sqrt{x}-81=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=3\\\sqrt{x}=-\dfrac{27}{7}\left(loại\right)\end{matrix}\right.\Leftrightarrow x=9\left(nhận\right)\)
 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !






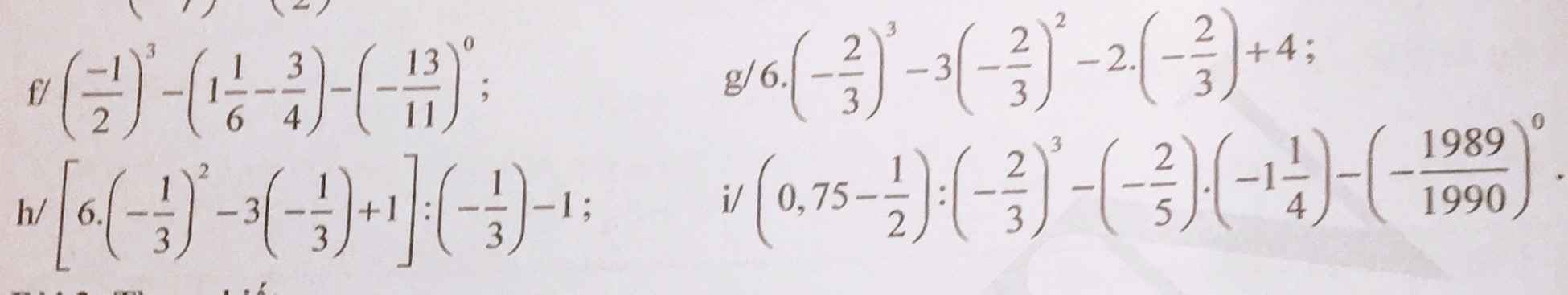
gợi ý thôi nha! Lười tb quá :D
a/ Khi khoá k mở, ta có sđmđ:
\(R_4nt\left[R_2//\left(R_1ntR_3\right)\right]ntR_5\)
\(\Rightarrow R=R_4+\frac{R_2.\left(R_1+R_3\right)}{R_2+R_1+R_3}+R_5=...\)(tự thay số) (1)
Có \(R=\frac{U}{I}=...\) (cái này bt U và I rùi thì thay vào) (2)
Có (1)=(2)=> R3=...(tự biến đổi, lúc này có mỗi R3 là ẩn)
b/ Lúc này khoá k đóng, ta có sđmđ:
\(\left\{\left[\left(R_1//R_4\right)ntR_2\right]//R_3\right\}ntR_5\)
\(\Rightarrow R=\frac{\left(\frac{R_1.R_4}{R_1+R_4}+R_2\right).R_3}{\frac{R_1.R_4}{R_1+R_4}+R_2+R_3}=...\) (lúc này bt R3 rùi thì thay vào)
\(\Rightarrow I_A=\frac{U}{R}=...\) (tự thay số)
Sau đó đi tính I2 và I4
Nếu I2>I4\(\Rightarrow\) dòng điện đi xuống\(\Rightarrow I_1=I_2-I_4=...\) \(\Rightarrow I_{A1}=I_1+I_3\)
Nếu \(I_2< I_4\Rightarrow\) dòng điện đi lên\(\Rightarrow I_1=I_4-I_2=...\Rightarrow I_{A1}=I_3-I_1\)
P/s: sơ đò mđ câu b bn tự vẽ nhé, chập 2 đầu ampe kế A1 vào là OK