Cho tam giác ABC. Vẽ phía ngoài các tam giácABC vuông tại A là ABD, ACE có AB=AD, AC=AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. C/M:a) DM=AHb)EN=AH. Có nhận xét gì về DM và EN.c) Gọi O là giao điểm của AN và DE. CM : O là trung điểm của DE CÁC BẠN GIÚP ĐỠ MÌNH NHA ! MÌNH CẦN GẤP LẮM. THANK YOU VERY MUCH...
Đọc tiếp
Cho tam giác ABC. Vẽ phía ngoài các tam giácABC vuông tại A là ABD, ACE có AB=AD, AC=AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. C/M:
a) DM=AH
b)EN=AH. Có nhận xét gì về DM và EN.
c) Gọi O là giao điểm của AN và DE. CM : O là trung điểm của DE
CÁC BẠN GIÚP ĐỠ MÌNH NHA ! MÌNH CẦN GẤP LẮM. THANK YOU VERY MUCH :::::)))))
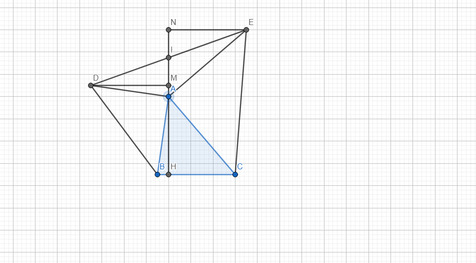
a) Ta có ˆBAH+ˆBAD+ˆDAM=180∘BAH^+BAD^+DAM^=180∘ (kề bù)
Mà ˆBAD=90∘⇒ˆBAH+ˆDAM=90∘BAD^=90∘⇒BAH^+DAM^=90∘ (1)
Trong tam giác vuông AMD, ta có:
ˆAMD=90∘⇒ˆDAM+ˆADM=90∘(2)AMD^=90∘⇒DAM^+ADM^=90∘(2)
Từ (1) và (2) suy ra: ˆBAH=ˆADMBAH^=ADM^
Xét hai tam giác vuông AMD và BHA, ta có:
ˆAMD=ˆBAH=90∘AMD^=BAH^=90∘
AB = AD (gt)
ˆBAH=ˆADMBAH^=ADM^ (chứng minh trên)
Suy ra: ∆AMD = ∆BHA (cạnh huyền, góc nhọn)
Vậy: AH = DM (2 cạnh tương ứng) (3)
b) Ta có: ˆHAC+ˆCAE+ˆEAN=180∘HAC^+CAE^+EAN^=180∘ (kề bù)
Mà ˆCAE=90∘(gt)⇒ˆHAC+ˆEAN=90∘CAE^=90∘(gt)⇒HAC^+EAN^=90∘ (4)
Trong tam giác vuông AHC, ta có:
ˆAHC=90∘⇒ˆHAC+ˆHCA=90∘(5)AHC^=90∘⇒HAC^+HCA^=90∘(5)
Từ (4) và (5) suy ra: ˆHCA=ˆEANHCA^=EAN^
Xét hai tam giác vuông AHC và ENA, ta có:
ˆAHC=ˆENA=90∘AHC^=ENA^=90∘
AC = AE (gt)
ˆHCA=ˆEANHCA^=EAN^ (chứng minh trên)
Suy ra: ∆AHC = ∆ENA (cạnh huyền, góc nhọn)
Vậy AH = EN (2 cạnh tương ứng)
Từ (3) và (6) suy ra : DM = EN
Vì DM⊥AHDM⊥AH và EN⊥AHEN⊥AH nên DM // EN (2 đường thẳng cùng vuông góc đường thẳng thứ 3)
Gọi O là giao điểm MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
ˆDMO=ˆENO=90∘DMO^=ENO^=90∘
DM = EN (chứng minh trên)
ˆMDO=ˆNEOMDO^=NEO^ (so le trong)
Suy ra: ∆DMO = ∆ENO (g.c.g) => OD = DE
Vậy MN đi qua trung điểm của DE.
bài này dễ mà , bình thường thôi . Bạn tự làm đi nha.