Biết F(x)=(ax2+bx+c)ex là một nguyên hàm của hàm số f(x)=(x-1)2.ex .Tính...
Đọc tiếp
Biết F(x)=(ax2+bx+c)ex là một nguyên hàm của hàm số f(x)=(x-1)2.ex .Tính S=a+2b+c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 7 2017
Chọn C
Phương pháp:
- Hàm số F (x) là một nguyên hàm của f (x) nếu F’ (x) =f (x) .
- Đồng nhất hệ số tìm a,b,c .
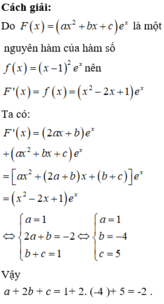
CM
18 tháng 12 2019
Ta có f x = 4 x 2 + 4 x + 3 2 x + 1 dx
= ∫ 2 x + 1 + 2 2 x + 1 d x = x 2 + x + ln x + 1 + C
Do f(0) = 1 nên c = 1. Suy ra f x = x 2 + x + ln 2 x + 1 + 1
Vậy a : b : c = 1 : 1 : 1
Đáp án B
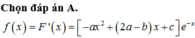
\(F\left(x\right)=\left(ax^2+bx+c\right)e^x\)
\(\Rightarrow F'\left(x\right)=\left(2ax+b\right)e^x+e^x\left(ax^2+bx+c\right)=e^x\left(ax^2+\left(2a+b\right)x+b+c\right)\)
Mà \(f\left(x\right)=\left(x^2-2x+1\right)e^x\)
Đồng nhất hệ số ta được:
\(\left\{{}\begin{matrix}a=1\\2a+b=-2\\b+c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-4\\c=5\end{matrix}\right.\) \(\Rightarrow S=-2\)