Cho hàm số y=f(x) có đạo hàm f'(x)=\(\frac{4}{x^2+1}\). Tính số giá trị nguyên của tham số m trong khoảng (-20;20) để hàm số g(x) = f(x) -mx +2 nghịch biến trên R?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


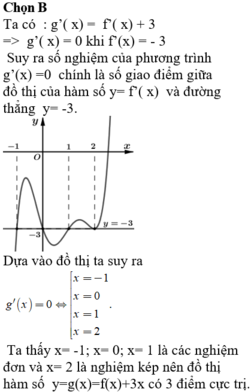
Đáp án A
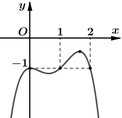
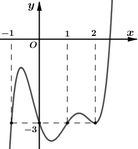
Dựa vào bảng biến thiên ta thấy rằng ![]() .
.
![]() đổi dấu khi qua hai điểm
đổi dấu khi qua hai điểm ![]() và
và ![]() không đổi dấu khi qua điểm x=1 nên hàm số y= f(x) có hai diểm cực trị.
không đổi dấu khi qua điểm x=1 nên hàm số y= f(x) có hai diểm cực trị.

Dựa vào bảng biến thiên ta thấy rằng f’(-2)=f’(1)=f’(3)=0.
f’(x)đổi dấu khi qua hai điểm x=-2; x=3 và f’(x) không đổi dấu khi qua điểm x=1 nên hàm số y=f(x) có hai diểm cực trị.
Đáp án A

Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng

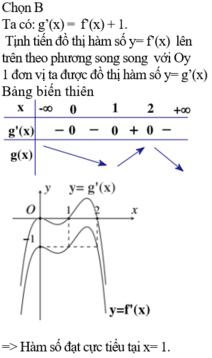
Ta có: f' (x - 2) = f' (x).(x-2)' = f'(x)
Do đó; đồ thị hàm số y= f’ (x) có hình dạng tương tự như trên.
Đồ thị hàm số y= f( x-2) có 3 điểm cực trị khi và chỉ khi đồ thị hàm số y= f( x) cũng có 3 điểm cực trị.
Chọn D.

Đáp án D
Phương pháp : Nhận xét : f’(x – 2) = f’(x)
Cách giải : Ta có : f’(x – 2) = (x – 2)’. f’(x) = f’(x) → Đồ thị hàm số y = f’(x) có hình dạng tương tự như trên.
Đồ thị hàm số y = f(x – 2)có 3 điểm cực trị => Đồ thị hàm số y = f(x) cũng có 3 điểm cực trị
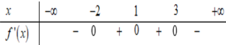




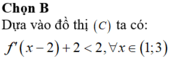


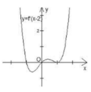
\(g'\left(x\right)=f'\left(x\right)-m=\frac{4}{x^2+1}-m\)
Để \(g\left(x\right)\) nghịch biến trên R \(\Leftrightarrow g'\left(x\right)\le0\) \(\forall x\in R\)
\(\Leftrightarrow\frac{4}{x^2+1}\le m\) \(\forall x\in R\) \(\Leftrightarrow m\ge\max\limits_{x\in R}f\left(x\right)\) với \(h\left(x\right)=\frac{4}{x^2+1}\)
Xét \(h'\left(x\right)=\frac{-8x}{\left(x^2+1\right)^2}=0\Rightarrow x=0\)
\(\Rightarrow h'\left(x\right)>0\) khi \(x< 0\); \(h'\left(x\right)< 0\) khi \(x>0\)
\(\Rightarrow x=0\) là điểm cực đại của hàm số \(h\left(x\right)\)
Dựa vào BBT ta thấy \(\max\limits_{x\in R}h\left(x\right)=h\left(0\right)=4\)
\(\Rightarrow m\ge4\) thì \(g\left(x\right)\) nghịch biến trên R
\(\Rightarrow\) Có \(20-4+1=17\) giá trị nguyên