Cho tam giác ABC vuông tại A, M là trung điểm của BC.CM \(AM=\frac{BC}{2}\).
Từ đó hãy chỉ ra rằng : Nếu \(\widehat{B}=30^0\) thì AC = \(\frac{BC}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


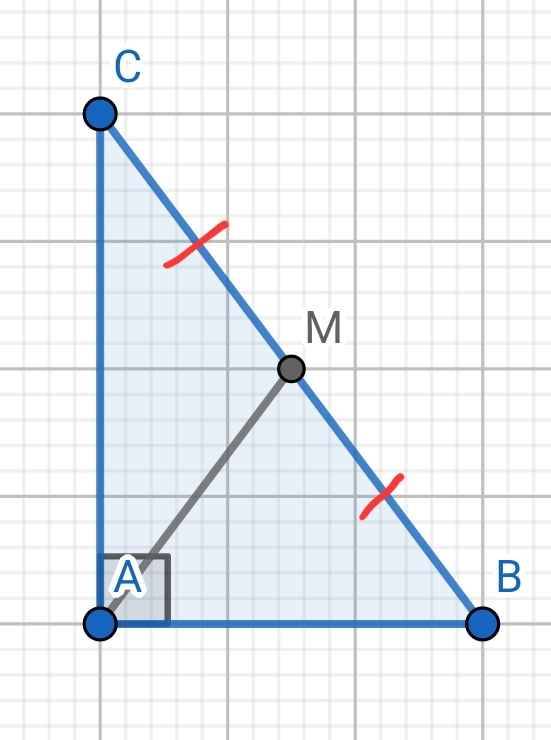
a) ∆ABC vuông tại A
M là trung điểm BC
⇒ AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
b) ∆ABC vuông tại A có ∠C = 30⁰
⇒ ∠B = 90⁰ - 30⁰ = 60⁰
Do AM = BM (cmt)
⇒ ∆ABM cân tại M
Lại có ∠ABM = ∠B = 60⁰
⇒ ∆ABM đều
⇒ AB = AM = BM = BC : 2

GT: Δ ABC vuông tại A
BM = CM
D ϵ tia đối của tia MA sao cgo MA = MD
KL: AD = BC
\(AM=\frac{1}{2}BC\)
Ta có hình vẽ:
Nối đoạn BD
Xét Δ BMD và Δ CMA có:
BM = CM (gt)
BMD = CMA (đối đỉnh)
MD = MA (gt)
Do đó, Δ BMD = Δ CMA (c.g.c)
=> BD = AC (2 cạnh tương ứng) và BDM = MAC (2 góc tương ứng)
Mà BDM và MAC là 2 góc so le trong nên BD // AC
=> BAC + ABD = 180o (trong cùng phía)
=> 90o + ABD = 180o
=> ABD = 180o - 90o = 90o = BAC
Xét Δ ABD và Δ BAC có:
BD = AC (cmt)
ABD = BAC = 90o
AB là cạnh chung
Do đó, Δ ABD = Δ BAC (c.g.c)
=> AD = BC (2 cạnh tương ứng) (1)
Mà AM = MD = \(\frac{1}{2}AD\) (2)
Từ (1) và (2) => \(AM=\frac{1}{2}BC\left(đpcm\right)\)

a: Gọi D là điểm đối xứng của A qua M
Xét tứ giác ABDC có
M là trung điểm của đường chéo BC
M là trung điểm của đường chéo AD
Do đó: ABDC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: AD=BC
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}BC\)

Để chứng minh ΔMAB = ΔMAC, ta có thể sử dụng nguyên lý cắt giao. Vì AB = AC và M là trung điểm BC, nên ta có AM là đường trung trực của đoạn thẳng BC. Từ đó, ta có AM ⊥ BC. Vì AM là đường trung trực của đoạn thẳng BC, nên ta cũng có MB = MC. Như vậy, ta đã chứng minh được ΔMAB = ΔMAC.
Để chứng minh AM là tia phân giác của góc BAC, ta có thể sử dụng tính chất của tam giác cân. Vì AB = AC và AM là đường trung trực của đoạn thẳng BC, nên ta có AM là tia phân giác của góc BAC.
Để chứng minh AM ⊥ BC, ta đã chứng minh ở trên rồi. Vì AM là đường trung trực của đoạn thẳng BC, nên ta có AM ⊥ BC.
trên tia đối của MA lấy MD sao cho MA = MD
xét tam giác CMD và tam giác BMA có : BM = MC do M là trung điểm của BC (gt)
góc AMB = góc CMD (đối đỉnh)
=> tam giác CMD = tam giác BMA (c-g-c)
=> CD = AB và góc CDM = góc MAB (đn)
mà góc CDM so le trong với MAB
=> CD // AB (đl)
=> góc BAC = góc ACD (đl)
mà góc BAC = 90 (gt)
=> góc BAC = góc ACD = 90
xét tam giác ABC và tam giác CDAcó : AC chung
CD = AB (cmt)
=> tam giác ABC = tam giác CDA (2cgv)
=> góc CDA = góc ABC mà góc CDA = góc DAB (cmt)
=> góc MAB = góc MBA (tcbc)
=> tam giác AMB cân tại M (đn)
=> MA = MB mà MB = BC/2 do M là trung điểm
=> MA = BC/2