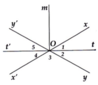
Cho hai đường thẳng xx' và yy' cắt nhau tại O , tia Ot là tia phân giác của gốc xOy
a) Gọi tia Ot' là tia đối của tia Ot. So sánh góc xOt' và t'Oy
b) Vé tia Om là tia phân giác của góc x'Oy. Tính góc mOt
HELP ME! Làm hộ mk vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
xOt = yOt ( Ot là phân giác )
x′Ot′=y′Ot′ ( Ot' là tia phân giác )
Vì Ot và Ot' là 2 tia phân giác đối nhau nên xOy và x′Oy′ là 2 góc đối đỉnh
Ta có :
xOy=x′Oy′ (cmt)
⇒xOy′=x′Oy
Từ đây ta thấy :
y′Ot′=x′Ot′
xOy′=x′Oy
nên xOy′+y′Ot′=x′Oy+x′Ot′
⇒xOt′ = t'Oy
b )
Ta có :
xOt=yOt=x′Ot′=y′Ot′
Vì Om là tia phân giác của x′Oy nên Om cũng là tia phân giác của tOt' .
Ta lại có :
tOt′=1800 ( 2 tia đối )
⇒mOt = 900
Ta có :
xOt=yOt ( Ot là phân giác )
x′Ot′=y′Ot′ ( Ot' là tia phân giác )
Vì Ot và Ot' là 2 tia phân giác đối nhau nên xOy và x′Oy′ là 2 góc đối đỉnh
Ta có :
xOy=x′Oy′ (cmt)
⇒xOy′=x′Oy
Từ đây ta thấy :
y′Ot′=x′Ot′
xOy′=x′Oy
nên xOy′+y′Ot′=x′Oy+x′Ot′
⇒xOt′=yOt′
b )
Ta có :
xOt=yOt=x′Ot′=y′Ot′
Vì Om là tia phân giác của x′Oy nên Om cũng là tia phân giác của tOt' .
Ta lại có :
tOt′=1800 ( 2 tia đối )
⇒tOm=900

x O y ' ^ = x ' O y ^
a) Ta có: O 1 ^ = x O y ^ 2
Mà O 1 ^ = O 2 ^ (đối đỉnh), x O y ^ = x ' O y ' ^ (đối đỉnh)
O 4 ^ = O 5 ^ Lại có:
x O t ' ^ = x O y ' ^ + O 5 ^ và t ' O y ^ = x ' O y ^ + O 4 ^ =
mà x O y ' ^ = x ' O y ^ (đối đỉnh) và O 4 ^ = O 5 ^
Lại có
x O t ' ^ = x O y ' ^ + O 5 ^ và t ' O y ^ = x ' O y ^ + O 4 ^
Mà x O y ' ^ = x ' O y ^ (đối đỉnh)
Và O 4 ^ = O 5 ^ => x O t ' ^ = t ' O y ^

Ta có: \(\widehat{xOy}=\widehat{x'Oy'}\)(đối đỉnh)
\(\Rightarrow\widehat{yOt}=\widehat{yOt'}\) (đối đỉnh)
Ta có: \(\widehat{xOy}+\widehat{xOy'}=\widehat{tOy'}+\widehat{tOy}=180^o\)
\(\Rightarrow\widehat{tOy}+\widehat{y'Ot'}=\widehat{tOt'}=180^o\)
Lại có: Hai góc đối nhau tao thành góc bẹt 180 độ.
Vậy: Ot và Ot' đối nhau (đpcm)

ta có: xx' cắt yy' tại O
=> góc xOy = góc x'Oy' ( đối đỉnh)
=> góc xOy/2 = góc x'Oy'/2
mà góc O1 = góc xOy/2 ( định lí tia phân giác)
góc O2 = góc xOy/2 ( định lí tia phân giác)
=> góc O1 = góc O2
mà góc O1 = góc xOy/2 => góc O1. 2 = góc xOy
mà góc xOy + góc xOy' = 180 độ
=> góc O1 .2 + góc xOy' = 180 độ
góc O1 + góc O1 + góc xOy' = 180 độ
=> góc O1 + góc O2 + góc xOy' = 180 độ ( góc O1 = góc O2)
=> Ot' là tia đối của tia Ot ( định lí)
a) Vì Ot là tia phân giác của \(\widehat{xOy}\)nên \(\widehat{xOt}=\widehat{tOy}=\frac{\widehat{xOy}}{2}\)
Ta có: \(\hept{\begin{cases}\widehat{xOt'}+\widehat{xOt}=180^0\\\widehat{t'Oy}+\widehat{yOt}=180^0\end{cases}}\)
Mà \(\widehat{xOt}=\widehat{tOy}\left(cmt\right)\)nên \(\widehat{xOt'}=\widehat{t'Oy}\left(đpcm\right)\)
b) Vì Ot là tia phân giác của \(\widehat{xOy}\)nên \(\widehat{xOt}=\widehat{tOy}=\frac{\widehat{xOy}}{2}\)
Vì Om là tia phân giác của \(\widehat{x'Oy}\)nên \(\widehat{x'Om}=\widehat{mOy}=\frac{\widehat{x'Oy}}{2}\)
Mà \(\widehat{xOy}+\widehat{x'Oy}=180^0\)(kề bù) nên \(\widehat{tOy}+\widehat{mOy}=\frac{180^0}{2}\)
\(\Rightarrow\widehat{mOt}=90^0\)
Vậy \(\widehat{mOt}=90^0\)