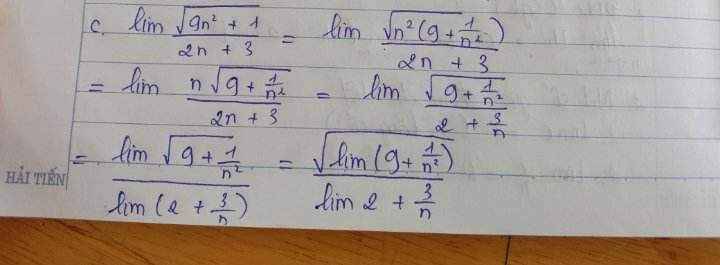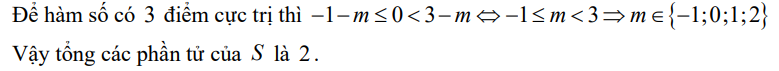ai giảng mình bài này với ạ, mình không hiểu lắm í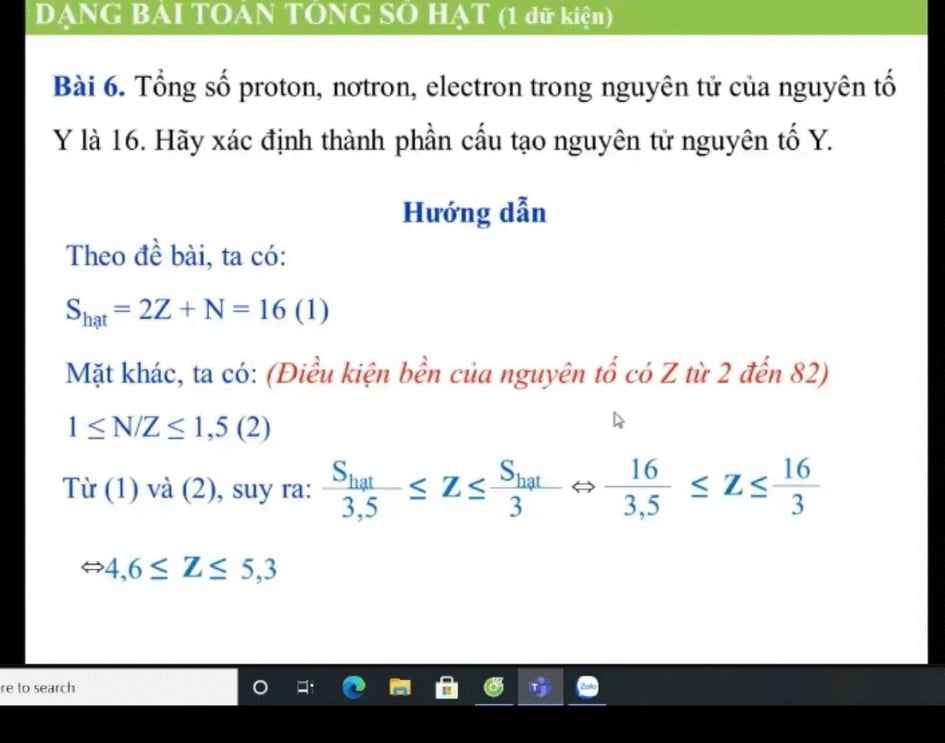
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HS
0
Những câu hỏi liên quan
NT
0
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 8 2021
Đây là 1 lời giải sai em
Đơn giản vì phương trình gốc không thể giải được
MC
Làm giúp mình bài này với ạ, mik không hiểu đề lắm ạ.
1
E
0
9 tháng 6 2021
(Dòng khoanh đỏ ở dấu tương đương đầu tiên)Có nghĩa là chia cả hai vế cho \(\dfrac{5\pi}{3}\) ấy
(Dòng khoanh đỏ ở dấu tương đương thứ hai) Xét \(cos\pi x=\dfrac{1}{10}+k\dfrac{6}{5}\) (*)
Do \(-1\le cos\pi x\le1\)\(\Leftrightarrow-1\le\dfrac{1}{10}+k\dfrac{6}{5}\le1\)
\(\Leftrightarrow-\dfrac{11}{12}\le k\le\dfrac{3}{4}\) mà k nguyên \(\Rightarrow k=0\)
Thay k=0 vào (*)\(\Rightarrow cos\pi x=\dfrac{1}{10}\)
Làm tương tự với cái bên dưới \(-1\le\dfrac{1}{2}+k\dfrac{6}{5}\le1\) \(\Leftrightarrow-\dfrac{5}{4}\le k\le\dfrac{5}{12}\Rightarrow\left[{}\begin{matrix}k=0\\k=-1\end{matrix}\right.\)
Thay k=0 với k=-1 sẽ ra được \(\left[{}\begin{matrix}cos\pi x=\dfrac{1}{2}\\cos\pi x=-\dfrac{7}{10}\end{matrix}\right.\)
(Với mỗi \(cos\pi x\) sẽ nhận được hai họ nghiệm => Tổng tất cả là 6 họ nghiệm)
HP
9 tháng 6 2021
Vì \(cosx\in\left[-1;1\right]\Rightarrow\left[{}\begin{matrix}-1\le\dfrac{1}{10}+k\dfrac{6}{5}\le1\left(1\right)\\-1\le\dfrac{1}{2}+k\dfrac{6}{5}\le1\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow-\dfrac{11}{12}\le k\le\dfrac{9}{12}\Leftrightarrow k=0\Rightarrow cosx=\dfrac{1}{10}\)
\(\left(2\right)\Leftrightarrow-\dfrac{15}{12}\le k\le\dfrac{5}{12}\Leftrightarrow\left[{}\begin{matrix}k=0\\k=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=-\dfrac{7}{10}\end{matrix}\right.\)
5 tháng 9 2016
Thanh Vy k nên làm như vậy nhé, x để vế trái tốt nhất, chỉ đối các số hạng đã biết thôi, nếu đổi -x qua phải rất
khó hiểu
5 tháng 9 2016
Lê Nguyên Hạo Không khó hiểu đâu. Chuyển -x qua vế phải và chuyển -6/7 qua vế trái , khi đó bài toán nhìn sẽ gọn hơn và bạn cũng không cần phải đổi dấu của x ở bước cuối cùng.
BB
1
H
29 tháng 5 2023
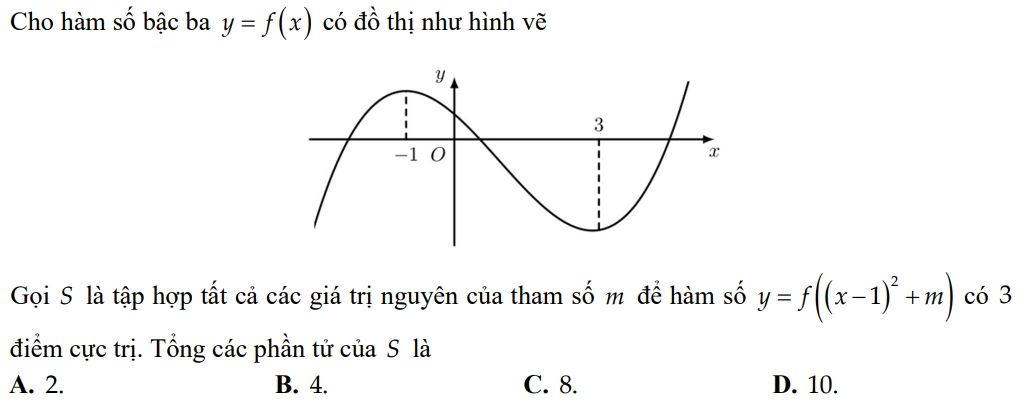
Bài này làm khá tắt chỗ 3 điểm cực trị, mình trình bày lại để bạn dễ hiểu nhé!
.......
Để y' = 0\(\Leftrightarrow\left[{}\begin{matrix}x=1\\f'\left(\left(x-1\right)^2+m\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2+m=-1\\\left(x-1\right)^2+m=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2=-1-m\left(1\right)\\\left(x-1\right)^2=3-m\left(2\right)\end{matrix}\right.\)
Để hàm số có 3 điểm cực trị thì y' = 0 có 3 nghiệm phân biệt.
Ta có 2 trường hợp.
+) \(TH_1:\) (1) có nghiệm kép x = 1 hoặc vô nghiệm và (2) có hai nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m\le0\\3-m>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m\ge-1\\m< 3\end{matrix}\right.\) \(\Leftrightarrow-1\le m< 3\)
+) \(TH_2:\) (2) có nghiệm kép x = 1 và (2) có một nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m>0\\3-m\le0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m\ge3\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)
\(\Rightarrow-1\le m< 3\Rightarrow S=\left\{-1;0;1;2\right\}\)
Do đó tổng các phần tử của S là \(-1+0+1+2=2\)
DN
2
8 tháng 11 2021
Bài 4:
\(a,A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\\ P=A:B=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{x-1}{\sqrt{x}+1}=\dfrac{x-1}{\sqrt{x}}\\ b,P\sqrt{x}=m-\sqrt{x}+x\\ \Leftrightarrow x-1=m-\sqrt{x}+x\\ \Leftrightarrow m=\sqrt{x}-1\)