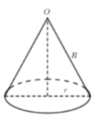
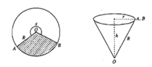
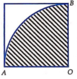
Bác A có một miếng thép mỏng tâm O với bán kính 4dm . Bác định cắt ra mọit hình quạt tròn tâm O rồi ghép 2 mép lại với nhau thành một vật có dạng hình nóng tròn xoay . Dung tích lớn nhất của vật mà bác A định tạo ra là bao nhiêu ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 5 2018
Diện tích hình tròn S = πR 2
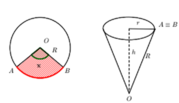
Gọi bán kính đường tròn đáy hình nón là r(0<r<R) ta có
Xét hàm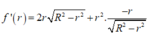 
có 
Bảng biến thiên:
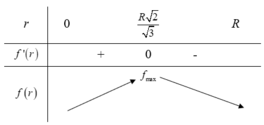
Do đó thể tích V đạt GTLN tại
r
=
R
2
3
. Khi đó
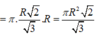
Vậy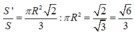 
Chọn đáp án D.
CM
15 tháng 5 2019
Đáp án D
Phương pháp:
- Lập hàm tinh thể tích khối nón, xét hàm suy ra GTLN.
- Tính diện tích S , S ' với chú ý S là diện tích hình tròn và S ' là diện tích xung quanh của hình nón.
CM
4 tháng 6 2019
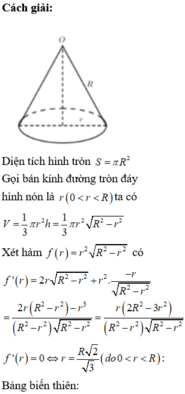
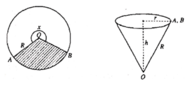
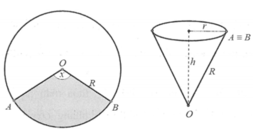
Thể tích cái phễu là V = 1 3 πr 2 h
Ta có chu vi đáy là 2 πr = Rx
Suy ra
r = R x 2 π h = R 2 - r 2 = R 2 - R 2 x 2 4 π 2 = R 2 π 4 π 2 - x 2
Áp dụng bất đẳng thức AM-GM cho 2 số dương ta có:
V = 3 R 3 48 π 2 x 2 . 2 3 π 4 π 2 - x 2 ≤ 3 R 3 2 . 48 π 2 x 2 4 3 π 2 + 4 π 2 - x 2 = 3 R 3 2 . 48 π 2 x 2 16 3 π 2 - x 2 ≤ 1 8 3 R 3 48 π 2 . x 2 + 16 3 π 2 - x 2 2 = 1 8 3 R 3 48 π 2 . 16 2 9 π 4 = 2 3 27 πR 3
Dấu bằng có khi và chỉ khi
2 3 π = 4 π 2 - x 2 x 2 = 16 3 π 2 - x 2 ⇔ x = 2 2 3 π
Vậy 2 3 27 πR 3 khi và chỉ khi x = 2 2 3 πR 3
Đáp án A
CM
21 tháng 11 2018
Đáp án D.
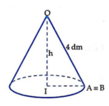
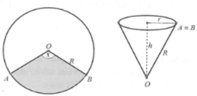
Cung AB có bán kính O A = 4 d m và số đo bằng π 2 r a d nên có độ dài là l A B = π 2 .4 = 2 π d m .
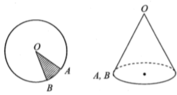
Từ giả thiết ta có đỉnh của hình nón là O, đường sinh O A = 4 d m và chu vi đáy hình nón là C = l A B = 2 π d m .
Gọi I là tâm đáy, khi đó bán kính đáy của hình nón là r = I A = C 2 π = 2 π 2 π = 1 (dm).
Do vuông tại I nên ta có O A 2 = O I 2 + I A 2 ⇒ h = O I = O A 2 − I A 2
⇒ h = 4 2 − 1 2 = 15 ≈ 3,873 (dm).
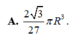
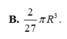
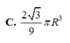
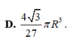
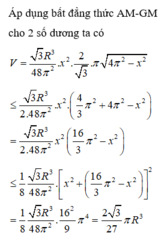
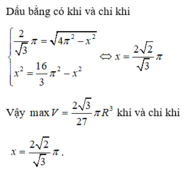
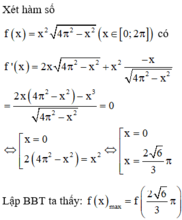
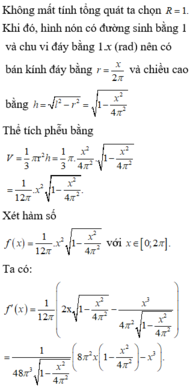
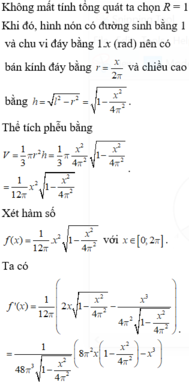
đặt chiều cao chóp = h
=> r đáy=\(\sqrt{4^2-h^2}\)
V = 1/3.h.(42-h2)\(\pi\)
đặt h.(4-h^2) là g(h)
=> bài toán trở thành tìm h ( 0<h<4) để g(h) max
=> 2 cách: tính đạo hàm hoặc chạy mode 7
=> hàm max tại h=\(\frac{4\sqrt{3}}{3}\)
=> V max=\(\frac{128\sqrt{3}}{27}\pi\)
v