Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.có 18 HLP nhỏ có mặt được sơn xanh,1 HLP nhỏ có 1 mặt sơn xanh
b.có 24 HLP nhỏ được sơn đỏ ,có 12 HLP nhỏ đc sơn đỏ 2 mặt,12 HLP nhỏ đc sơn đỏ 1 mặt
c. có 3 HLP nhỏ không đc sơn mặt nào
tích mình nhé :D thanks

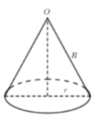
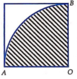
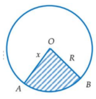
Diện tích hình tròn S = πR 2
Gọi bán kính đường tròn đáy hình nón là r(0<r<R) ta có
![]()
Xét hàm 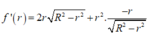
có 

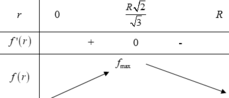
Bảng biến thiên:
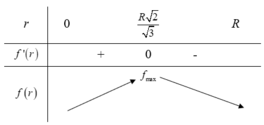
Do đó thể tích V đạt GTLN tại
r
=
R
2
3
. Khi đó
![]()
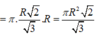
Vậy 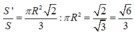
Chọn đáp án D.

Đáp án D
Phương pháp:
- Lập hàm tinh thể tích khối nón, xét hàm suy ra GTLN.
- Tính diện tích S , S ' với chú ý S là diện tích hình tròn và S ' là diện tích xung quanh của hình nón.
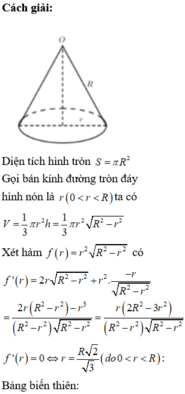
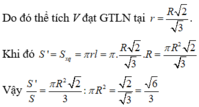

Đáp án D
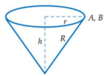
Gọi r;h lần lượt là bán kính đáy và chiều cao của khối nón ⇒ V N = 1 3 π r 2 h
Mà h = l 2 − r 2 = R 2 − r 2 = 81 − r 2 Suy ra V N = 1 3 π r 2 81 − r 2 = π 3 r 4 81 − r 2
Ta có r 2 . r 2 . 162 − 2 r 2 2 ≤ r 2 + r 2 + 162 − 2 r 2 3 2.27 = 78732 ⇒ V ≤ π 3 . 78732 ⇒ V max = 78732 3 π
Dấu " = " xaye ra ⇔ 3 r 2 = 162 ⇔ r = 3 6 ⇒ Độ dài cung tròn là l = 2 π r = 6 π 6

Người thợ đó gấp đôi mảnh vải chia thành 2 phần, sau đó tiếp tục gấp đôi manh vải của mỗi mãnh vai trên chia thành 4 phần . Bây giờ người thợ đó cắt \(\dfrac{3}{4}\) mảnh vải dựa theo 4 phần đã chia thì ta có 1 mảnh vải có diện tích 1m\(^2\).

Đáp án A
Phương pháp giải:
Tìm giá trị lớn nhất của thể tích khối nón và áp dụng công thức tính độ dài cùng tròn
Lời giải:
Gọi r, h lần lượt là bán kính đáy, chiều cao của phễu hình nón.
Thể tích của khối nón là 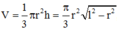 với l là độ dài đường sinh và l = R bán kính tấm bìa hình tròn =>
với l là độ dài đường sinh và l = R bán kính tấm bìa hình tròn => 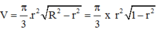 vì chuẩn hóa R = 1
vì chuẩn hóa R = 1
Xét hàm số ![]() trên (0;1) có
trên (0;1) có 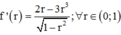
Ta có 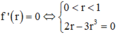
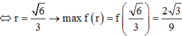
Do đó 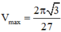 Dấu “=” xảy ra khi và chỉ khi
Dấu “=” xảy ra khi và chỉ khi 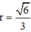
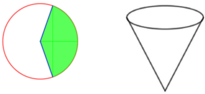
Mà độ dài cung phần cuộn làm phễu chính là chu vi đáy hình nón
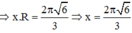



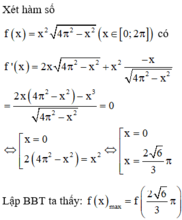
Đáp án D.
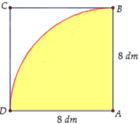
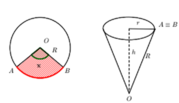
Cung AB có bán kính O A = 4 d m và số đo bằng π 2 r a d nên có độ dài là l A B = π 2 .4 = 2 π d m .
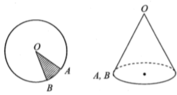
Từ giả thiết ta có đỉnh của hình nón là O, đường sinh O A = 4 d m và chu vi đáy hình nón là C = l A B = 2 π d m .
Gọi I là tâm đáy, khi đó bán kính đáy của hình nón là r = I A = C 2 π = 2 π 2 π = 1 (dm).
Do vuông tại I nên ta có O A 2 = O I 2 + I A 2 ⇒ h = O I = O A 2 − I A 2
⇒ h = 4 2 − 1 2 = 15 ≈ 3,873 (dm).