tìm min max của y = sin x trên đoạn \(\left[\frac{-\pi}{3};\frac{2\pi}{3}\right]\)
Cách lập bảng biến thiên để tìm min max ntn, chỉ rõ cách lập bảng biến thiên giúp mh đk k, cảm ơn nhé!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 9 2021
1, \(y=2-sin\left(\dfrac{3x}{2}+x\right).cos\left(x+\dfrac{\pi}{2}\right)\)
\(y=2-\left(-cosx\right).\left(-sinx\right)\)
y = 2 - sinx.cosx
y = \(2-\dfrac{1}{2}sin2x\)
Max = 2 + \(\dfrac{1}{2}\) = 2,5
Min = \(2-\dfrac{1}{2}\) = 1,5
2, y = \(\sqrt{5-\dfrac{1}{2}sin^22x}\)
Min = \(\sqrt{5-\dfrac{1}{2}}=\dfrac{3\sqrt{2}}{2}\)
Max = \(\sqrt{5}\)
HP
18 tháng 9 2021
\(y=sin\left(x+\dfrac{\pi}{3}\right)-sinx\)
\(=\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx-sinx\)
\(=\dfrac{\sqrt{3}}{2}cosx-\dfrac{1}{2}sinx\)
\(=cos\left(x+\dfrac{\pi}{6}\right)\in\left[-1;1\right]\)
\(\Rightarrow\left\{{}\begin{matrix}y_{mịn}=-1\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\\y_{max}=1\Leftrightarrow x=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
NP
1
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Vẽ đồ thị:
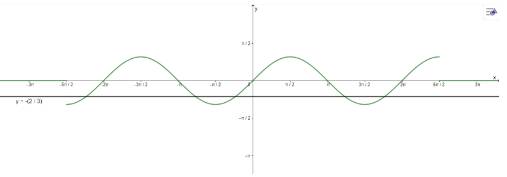
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:
\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm
NL
1
TA
22 tháng 5 2021
ĐK: Biểu thức xác định với mọi `x`.
`y_(min) <=> (\sqrt(2-cos(x-π/6))+3)_(max) <=> (cos(x-π/6))_(max)`
`<=> cos(x-π/6)=1 <=> x-π/6=k2π <=> x = π/6+k2π ( k \in ZZ)`.
`=> y_(min) = 1`
`y_(max) <=> (\sqrt(2-cos(x-π/6))+3)_(min) <=> (cos(x-π/6))_(min)`
`<=> cos(x-π/6)=-1 <=> x -π/6= π+k2π <=> x = (7π)/6+k2π (k \in ZZ)`
`=> y_(max) = (6-2\sqrt3)/3`.
A
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 7 2020
Chắc đề là \(y=1+\sqrt{3}sin^2\left(x-\frac{\pi}{3}\right)\)
Do \(sin^2\left(x-\frac{\pi}{3}\right)\ge0;\forall x\Rightarrow y\ge1\)
\(y_{min}=1\) khi \(sin\left(x-\frac{\pi}{3}\right)=0\)
\(\Leftrightarrow x-\frac{\pi}{3}=k\pi\Rightarrow x=\frac{\pi}{3}+k\pi\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta có
\(\begin{array}{l}\sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \sin \left( {\frac{\pi }{4}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{4}{\rm{ }} = {\rm{ }}\frac{\pi }{4} + k2\pi ;k \in Z\\x + \frac{\pi }{4}{\rm{ }} = {\rm{ }}\pi {\rm{ - }}\frac{\pi }{4} + k2\pi ;k \in Z\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = {\rm{ }}k2\pi ;k \in Z\\x{\rm{ }} = {\rm{ }}\frac{\pi }{2} + k2\pi ;k \in Z\end{array} \right.\end{array}\)
Mà \(x \in \left[ {0;\pi } \right]\) nên \(x \in \left\{ {0;\frac{\pi }{2}} \right\}\)
Vậy phương trình đã cho có số nghiệm là 2.
Chọn C
\(y'=cosx\) ; \(y'=0\Rightarrow cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\)
Do \(x\in\left[-\frac{\pi}{3};\frac{2\pi}{3}\right]\Rightarrow x=\frac{\pi}{2}\)
Không cần lập bảng biến thiên, chúng ta chỉ cần quan tâm 3 vị trí: 2 biên và điểm dừng vừa tìm được
\(y\left(\frac{\pi}{2}\right)=1\) ; \(y\left(-\frac{\pi}{3}\right)=-\frac{\sqrt{3}}{2}\) ; \(y\left(\frac{2\pi}{3}\right)=\frac{\sqrt{3}}{2}\)
So sánh 3 giá trị trên ta được:
\(y_{max}=1\) khi \(x=\frac{\pi}{2}\)
\(y_{min}=-\frac{\sqrt{3}}{2}\) khi \(x=-\frac{\pi}{3}\)