cho đường thẳng d cắt đường tròn(O;R)tại 2 điểm C,D.M là 1 điểm thuộc d và nằm ngoài (O:R)(MC<MD).vẽ 2 tiếp tuyến MA,MB với (O:R).H là trung điểm của CD.Đường thẳng AB cắt OH tại E.Chứng minh khi M di động trên d thì đường thẳng AB luôn đi qua 1 điểm cố định
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 3 2020
Ta có : \(\widehat{IBA}+\widehat{ICB}=90^o\)
\(\widehat{IAB}+\widehat{IAO}+\widehat{OAC}=180^o\)mà \(\widehat{IAO}=90^o\)\(\Rightarrow\widehat{IAB}+\widehat{OAC}=90^o\)
Mà \(OA=OC\Rightarrow\)\(\Delta OAC\)cân tại O \(\Rightarrow\widehat{OCA}=\widehat{OAC}\)
Từ đó suy ra \(\widehat{IAB}=\widehat{IBA}\Rightarrow\Delta IAB\)cân tại I
\(\Rightarrow IA=IB\)
13 tháng 4 2021
1: Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{ABC}=90^0\)
Xét (O') có
\(\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{ABD}=90^0\)
Ta có: \(\widehat{ABC}+\widehat{ABD}=\widehat{CBD}\)
\(\Leftrightarrow\widehat{CBD}=90^0+90^0=180^0\)
hay C,B,D thẳng hàng(đpcm)
CM
17 tháng 1 2019
a. b.
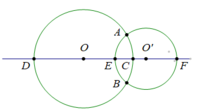
c. - Đường tròn (O’; 1cm) có đường kính là: EF; Các dây cung là: EA, EB, AB, FA, FB
Vì E thuộc (O’; 1cm) nên EO’=1cm; EF=2.EO’=2cm
- Đường tròn (O; 1,5cm) có đường kính là: DC; Các dây cung là: DA, DB, AB, AC, CB
Vì C thuộc (O; 1,5cm) nên CO=1,5cm; DC=2.CO=3cm
d. Vì đường tròn (O’; 1cm) cắt đoạn thẳng OO’ tại E, nên E nằm giữa 2 điểm O và O’.
Ta có: O E + E O ' = O O ' ⇒ O E = 1 c m
Mà EO’=1cm, nên OE=EO’ (=1cm)
Do đó: E là trung điểm của đợn thẳng OO’.
e. Vì đường tròn (O; 1cm) cắt đường thẳng OO’ tại D, đường tròn (O’; 1cm) cắt đường thẳng OO’ tại F, nên 4 điểm D, O, O’, F lần lượt theo thứ tự đó và DO=1,5cm; O’F=1cm.
Ta có: D F = D O + O O ' + O ' F = 1 , 5 + 2 + 1 = 4 , 5 c m .
Vậy DF=4,5cm
7 tháng 4 2023
a: Xét ΔABE và ΔADB co
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB/AD=AE/AB
=>AB^2=AD*AE
Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2=AE*AD
=>AH/AD=AE/AO
=>ΔAHE đồng dạng với ΔADO
=>góc AHE=góc ADO
=>góc OHE+góc ODE=180 độ
=>OHED nội tiếp
b: OHED nội tiếp
=>góc HED+góc HOD=180 độ
BD//AO
=>góc BDO+góc HOD=180 độ
=>góc BDO=góc HED
góc BCD+góc BDC=90 độ
góc BCD=góc BED
=>góc HED+góc BED=90 độ
=>HE vuông góc BF tại E
31 tháng 3 2021
a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
TA
10 tháng 5 2020
a) Kẻ OH ⊥⊥ d
=> OH là khoảng cách từ d tới tâm đường tròn (O)
mà OH < R (3 < 5)
=> Đường thẳng d cắt đường tròn (O)
b) Xét ΔΔOAH vuông tại H có:
OH2+AH2=OA2OH2+AH2=OA2 (ĐL Pi-ta-go)
=> AH=OA2−OH2−−−−−−−−−−√=52−32−−−−−−√=4(cm)AH=OA2−OH2=52−32=4(cm)
Xét (O): AB là dây, OH ⊥⊥ AB
=> H trung điểm AB (quan hệ ⊥⊥ giữa đường kính và dây cung)
=> AB = 2AH = 8(cm)
c) Xét ΔΔABC có: O, H trung điểm AC, AB
=> OH là đường trung bình ΔΔABC
=> OH // BC mà OH ⊥⊥ AH
=> BC ⊥⊥ AH => ΔΔABC vuông tại B
=> AB2 + BC2 = AC2
=> BC=102−82−−−−−−−√=6(cm)BC=102−82=6(cm)
Xét ΔΔABC vuông tại B
có: sinC=ABAC=810=45⇒Cˆ=53o7′sinC=ABAC=810=45⇒C^=53o7′
=> Aˆ=36o52′A^=36o52′
d) Xét ΔΔACM vuông tại C: CB ⊥⊥ AM
có: AC2=AB⋅AMAC2=AB⋅AM (HTL tam giác vuông)
=> AM=AC2AB=1028=12,5(cm)AM=AC2AB=1028=12,5(cm)
lại có: AB + BM = AM ; AB = 8(cm)
=> BM = 4,5(cm)
Mình không vẽ hình được bạn thông cảm nhé
Gọi K là giao điểm của OM và AB
Xét tam giác MBO vuông có
OK.OM=OB^2=R^2
VÌ H là trung điểm của CD
=> \(OH\perp CD\)
=> tam giác EKO đồng dạng tam giác MHO
=> OH.OE=OK.OM=R^2=OC^2
=> \(\frac{OH}{OC}=\frac{OC}{OE}\)
=> tam giác EHC đồng dạng tam giác ECO
=> ECO=90độ
=> EC là tiếp tuyến của đường tròn
CMTT ED là tiếp tuyến của đường tròn
MÀ C,D cố định
=> E cố định
=> AB đi qua E cố định
Vậy AB luôn đi qua một điểm cố định khi M di chuyển trên d