Tam giác ABC cân tại A có AB = AC = 50cm, BC = 60cm, các đường cao AD và CE cắt nhau tại H. Tính CH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi H là trung điểm BC suy ra BH = CH = 30cm
Do tam giác ABC cân tại A nên dễ dàng chứng minh được tam giác BEC = tam giác CDB (cgc)
=> BE = CD
mà AB = AC
nên AE = AD tức là tam giác AED cân tại A
Lại có: áp dụng định lý Pitago vào tam giác vuông AHC
ta tính được AH = 40cm
do đó diện tích tam giác ABC = S(ABC) = 1/2 . AH. BC = 1200
mà S(ABC) = 1/2 . BD. AC suy ra BD = 48cm
Áp dụng Pitago vào tam giác vuông ABD
tính được AD = 14cm
Mặt khác, do AD = AE và AB = AC
nên DE // BC
áp dụng định lý Ta-lét ta được: AD/AC = DE/BC
suy ra DE = 288/5

Đề sai nhé bạn nếu mà cho tam giác ABC cân tại A thì sẽ có AB=AC=50cm hoặc AB=AC=60 cm ko thể là AB=50 AC=60 nhé bạn :)
Mik viết sai đề nha bạn . đề là :Cho tam giác ABC cân tại A có AB=50cm, BC=60cm. Cac đường cao AD,CE cắt nhau tại H. Tính Ch

a: Ta có: ΔABC cân tại A
mà AD là đường cao
nên D là trung điểm củabC
=>BD=CD=30cm
AD=40cm
Xét ΔADC vuông tại D và ΔBEC vuông tại E có
góc C chung
Do đó: ΔADC đồng dạng với ΔBEC
Suy ra: DC/EC=AC/BC=AD/BE
=>30/EC=50/60=40/BE
=>30/EC=40/BE=5/6
=>EC=36cm; BE=48cm
b: Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
góc HBD chung
Do đó: ΔBDH đồng dạg với ΔBEC
Suy ra: BH/BC=BD/BE
=>BH/60=30/48=5/8
hay BH=37,5(cm)
=>CH=37,5cm

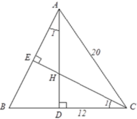
Tam giác ABC cân tại A nên B D = D C = B C 2 = 24 2 = 12 ( c m )
Theo định lý Py-ta-go, ta có A D 2 = A C 2 - D C 2 = 20 2 - 12 2 = 16 2
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
C D H ^ = A D B ^ = 90 ∘
C 1 = A 1 (cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên H D B D = H C A B = C D A D , tức là H D 12 = H C 20 = 12 16 = 3 4
Suy ra HD = 9cm.
Đáp án: C

b: Xét ΔABD vuông tại D và ΔCBE vuông tại E có
\(\widehat{B}\) chung
Do đó: ΔABD\(\sim\)ΔCBE

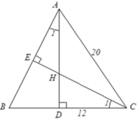
Tam giác ABC cân tại A nên B D = D C = B C 2 = 24 2 = 12 ( c m )
Theo định lý Py-ta-go, ta có A D 2 = A C 2 - D C 2 = 20 2 - 12 2 = 16 2
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
C D H ^ = A D B ^ = 90 ∘
C 1 = A 1 (cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên H D B D = H C A B = C D A D , tức là H D 12 = H C 20 = 12 16 = 3 4
Suy ra HD = 9cm => AH = AD - HD = 16 - 9 = 7cm
Đáp án: B
a) \(\Delta ABC\) cân nên đường cao AD cũng là trung tuyến => BD = DC = 30 cm
Áp dụng Pitago trong tam giác vuông ADB ta tính được AD = 40 cm
Ta giác vuông ABD ~ CHD (g.g)
=> \(\frac{AB}{CH}=\frac{AD}{CD}\) hay CH = \(\frac{AB.CD}{AD}=\frac{150}{4}\) cm
Xét \(\Delta ABD\) và \(\Delta CHD\) có :
\(\widehat{ADB}=\widehat{HDC}=90^o;\widehat{BAD}=\widehat{HCD}\) (cùng phụ với \(\widehat{ABD}\))
\(\Rightarrow\) \(\Delta ABD\) = \(\Delta CHD\)