Hai đường tròn có bán kính khác nhau ( O) và ( O') cắt nhau tại A và B. Tiếp tuyến tại A của (O') cắt (O) tại M. Tiếp tuyến tại A của ( O ) cắt (O') tại N. Gọi I là đường tròn ngoại tiếp tam giác MAN. ĐƯờng thẳng AB cắt (I) tại điểm thứ 2 là P. Chứng minh a, Tứ giác OAO'I là hình bình hành. b, Tứ giác OO'BI nội tiếp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) HS tự vẽ hình.
b) Hai đường tròn trên có đi qua O và I. Chúng có cắt nhau.

a) HS tự vẽ hình.
b) Hai đường tròn trên có đi qua O và I. Chúng có cắt nhau.

H la giao diem cua AB va CD ta co AH = BH =1/2 AB =12cm
cH=DH=6cm
=> AC=AD =\(\sqrt{12^2+6^2}\)=\(6\sqrt{5}\)......................

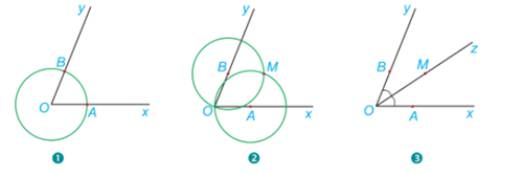
Xét \(\Delta OBM\) và \(\Delta OAM\) có:
\(OA = OB( = R)\)
OM chung
AM=BM (do hai đường tròn tâm A và B có bán kính bằng nhau)
\( \Rightarrow \)\(\Delta OBM\) = \(\Delta OAM\)(c.c.c)
\( \Rightarrow \) \(\widehat {MOB} = \widehat {MOA}\) (hai góc tương ứng)
Mà tia OM nằm trong góc xOy
Vậy OM là tia phân giác của góc xOy.

Vẽ lục giác đều ngoại tiếp đường tròn tâm O. Khi đó 6 đường tròn cần vẽ chính là các đường tròn nội tiếp các tam giác tạo thành từ O với 2 đỉnh kề nhau của lục giác ngoại tiếp đó.
Và ta có mỗi tam giác đó là tam đều nên tâm của 6 tam giác nhỏ chính là trọng tâm của các tam giác đều đó. Khi đó bán kính của 6 tam giác đó:
\(R=\frac{1}{3}.Ro=\frac{1}{3}.9=3\)