Chứng minh rằng : hàm số y=f(x)=1/2x+1 đồng biến trên R
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y=f\left(x\right)=6x-1-2x\sqrt{5}+\sqrt{5}=x\left(6-2\sqrt{5}\right)+\sqrt{5}-1\)
Vì \(6-2\sqrt{5}\ne0\) nên hs bậc nhất
Ta có \(6-2\sqrt{5}=\left(\sqrt{5}-1\right)^2>0\left(6-2\sqrt{5}\ne0\right)\) nên hs đồng biến trên R

Gọi x1, x2 là hai giá trị của x (x1>x2)
Ta có: x1>x2\(\Leftrightarrow\)-2x1<-2x2 \(\Leftrightarrow\)f(x1) < f(x2)
Vì x1>x2 mà f(x1) < f(x2) suy ra hàm số nghịch biến trên tập hợp số thực R

\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{-x_1+1+x_2-1}{x_1-x_2}=-1\)
Vậy: f(x) nghịch biến trên R

`a=m^2+m+1=m^2+2.m. 1/2 + (1/2)^2 + 3/4= (m+1/2)^2 + 3/4 >0 forall m`
`=> a>0 =>` Hàm số luôn đồng biến trên `RR`.
Để hàm số trên đồng biến khi \(m^2+m+1=m^2+m+\dfrac{1}{4}+\dfrac{3}{4}=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
Vậy hàm số luôn đồng biến trên R

Answer:
Ta có:
\(y=f\left(x\right)=6x-1-\sqrt{5}\left(2x-1\right)\)
\(=6x-1-2\sqrt{5}x+\sqrt{5}\)
\(=x.\left(6-2\sqrt{5}\right)+\left(\sqrt{5}-1\right)\)
Mà: Hàm số bậc nhất có dạng \(y=ax+b\) trong đó: \(a,b\inℝ;a\ne0\)
Ta thấy:
\(a=6-2\sqrt{5}\ne0\)
\(b=\sqrt{5}-1\inℝ\)
\(\Rightarrow x.\left(6-2\sqrt{5}\right)+\left(\sqrt{5}-1\right)\) là hàm số bậc nhất
\(\Rightarrow y=f\left(x\right)=6x-1-\sqrt{5}\left(2x-1\right)\) là hàm số bậc nhất
Ta thấy:
Hệ số \(a=6-2\sqrt{5}\)
Mà: Hàm số đồng biến khi hệ số \(a>0\) và nghịch biến khi \(a< 0\)
Thấy được:
\(6-2\sqrt{5}>0\)
\(\Rightarrow a=6-2\sqrt{5}>0\)
Vậy hàm số \(y=f\left(x\right)=6x-1-\sqrt{5}\left(2x-1\right)\) đồng biến trên \(ℝ\)

a) \(f\left(0\right)=\dfrac{2}{7}.0-8=-8\)
\(f\left(2\right)=\dfrac{3}{7}.2-8=-\dfrac{50}{7}\)
\(f\left(-1\right)=\dfrac{3}{7}.\left(-1\right)-8=-\dfrac{59}{7}\)
\(f\left(-2\right)=\dfrac{3}{7}.\left(-2\right)-8=-\dfrac{62}{7}\)
b) Với mọi \(x_1,x_2\in R\), ta có
\(x_1>x_2\Leftrightarrow\dfrac{3}{7}x_1>\dfrac{3}{7}x_2\Leftrightarrow\dfrac{3}{7}x_1-8>\dfrac{3}{7}x_2-8\Leftrightarrow f\left(x_1\right)>f\left(x_2\right)\)
\(\Rightarrow\) Hàm số luôn đồng biến trên R
b: Vì \(a=\dfrac{3}{7}>0\) nên hàm số đồng biến trên R

\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{3x_1-2-3x_2+2}{x_1-x_2}=3\)
Vậy: Hàm số đồng biến trên R
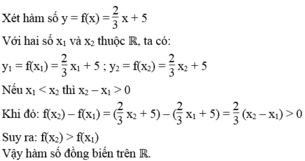
Với \(x_1;x_2\)bất kì thuộc \(ℝ\)và \(x_1< x_2\) Ta có :
\(f\left(x_1\right)=\frac{1}{2}x_1+1\)
\(f\left(x_2\right)=\frac{1}{2}x_2+1\)
\(\Rightarrow f\left(x_1\right)-f\left(x_2\right)=\frac{1}{2}\left(x_1-x_2\right)< 0\)
(Vì \(x_1< x_2\Rightarrow x_1-x_2< 0\))
\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
Vậy hàm số đồng biến trên \(ℝ\)