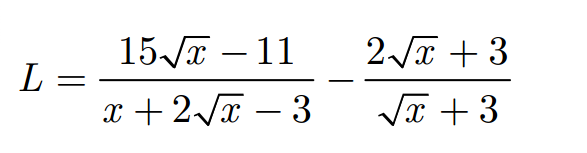Hãy rút gọn biểu thức sau biết ( n ; k) là số nguyên: (n+1).(n+2).(n+3).....(n+k)-k
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(-m+n-p\right)-\left(-m-n-p\right)\)
\(=-m+n-p+m+n+p\)
\(=\left(-m+m\right)+\left(-p+p\right)+\left(n+n\right)\)
\(=2n\)
Vậy \(\left(-m+n-p\right)-\left(-m-n-p\right)=2n\)
\(\left(-m+n-p\right)-\left(-m-n-p\right)\)
\(=-m+n-p+m+n+p\)
\(=\left(-m+m\right)+\left(-p-p\right)+\left(n+n\right)\)
\(=0+0+\left(n+n\right)\)
\(=0+\left(n+n\right)\)
\(=n+n\)
\(=2n\)
Vậy biểu thức (-m+n-p)-(-m-n-p) =2n



=(2a-3)3+(2a-3)2a+3^2-b
=6a-9+(2a)^2-6a+9-b
=6a-6a+9-9+(2a)^2-b
=(2a)^2-b

Ta có: \(L=\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\)
\(=\dfrac{15\sqrt{x}-11-\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{15\sqrt{x}-11-2x+2\sqrt{x}-3\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-2x+14\sqrt{x}-8}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)

\(=\left(3a-1\right)^2+2\left(3a-1\right)\left(3a+1\right)+\left(3a+1\right)^2\\ =\left(3a-1+3a+1\right)^2=\left(6a\right)^2=36a^2\)

=-m+n-p-m-n+m+p
(-m-m+m)+(n-n)+(-p+p)
(-m)+0+0=(-m)
TICH NHA