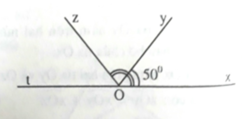
Trên cùng 1 nửa mặt phằng bờ chứa tia ox, vẽ tia Oy, Oz sao cho góc xOy = 50 độ, góc xOz = 130 độ
a. Tính yOz
b. Gọi Ot là tia p/g của yOz . tính yOt
c. Gọi Ox' là tia đối của Ox. Tính x'Oy và x'Ot
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 4 2021
a)vì các tia oy và oz cung nằm trên nửa mp bờ õ
mà xoy=50o xoz=130o
=> xoy<xoz
=> oy nằm giữa
ta có xoy+yoz=xoz
yoz=xoz-xoy=130o-50o=80o
26 tháng 4 2021
vì ot là tia pg của yoz
=>yot=toz=yoz/2 =80o/2=40o
=>xot=xoy+yot=50o+40o=90o
CM
3 tháng 11 2018
a) Trên cùng nửa mặt phẳng bờ chứa tia Ox có hai tia Oy, Oz và
25 tháng 7 2023
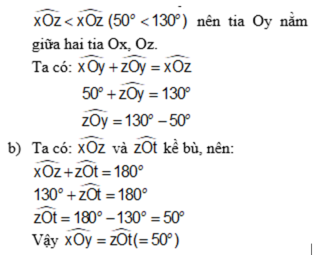
a: góc xOy<góc xOz
=>Oy nằm giữa Ox và Oz
=>góc xOy+góc yOz=góc xOz
=>góc yOz=65 độ
b: góc mOz=90-65=25 độ
c: góc zOt=180-115=65 độ
=>góc zOt=góc zOy
=>Oz là phân giác của góc tOy
3 tháng 4 2021
a) vì \(\widehat{xoy}< \widehat{xoz}\left(40^o< 120^o\right)\) nên ta có :
\(\widehat{xoz}=\widehat{xoy}+\widehat{yoz}\)
\(\Rightarrow\widehat{yoz}=\widehat{xoz}-\widehat{xoy}=120^o-40^o=130^o\)
vậy \(\widehat{yoz}=130^o\)
b) vì Tia Ot là tia đối của tia Oy nên \(\widehat{xot}\) và \(\widehat{xoy}\) là 2 góc kề bù,ta có:
\(\widehat{xot}+\widehat{xoy}=180^o\)
\(\Rightarrow\widehat{xot}=180^o-\widehat{xoy}=180^o-40^o=140^o\)
vậy:\(\widehat{xot}=140^o\)
c) Vẽ Om là tia phân giác của tia Oy(????) .. Tính số đo góc xOt . Chứng tỏ tia Oy là tia phần giác của góc xOm
(đề ko đc rõ 
)
26 tháng 3 2021
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(40^0< 120^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
\(\Leftrightarrow\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
\(\Leftrightarrow\widehat{yOz}+40^0=120^0\)
hay \(\widehat{yOz}=80^0\)
Vậy: \(\widehat{yOz}=80^0\)
" Bỏ bước vẽ hình nha"
a) Giải
Vì Oy và Oz cùng nằm trên 1 nửa mặt phẳng bờ chứa tia Ox
=> xOy < xOz ( 50độ < 130độ)
=> Tia Oy nằm giữa hai tia Ox và Oz
Vì tia Oy nằm giữa hai tia Ox và Oz
=> xOz - xOy = yOz
=> yOz = 130độ - 50độ
=> yOz = 80độ
b) Vì tia Ot là tia phân giác của yOz
=> tOz = yOt = yOz/2 = 40độ
=> yOt = yOz - 40độ
=> yOt = 40độ