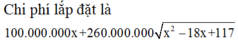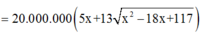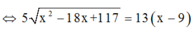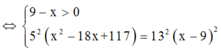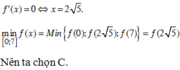Người ta giăng lưới để riêng một loại cá trên một góc hồ hình chữ nhật. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc cắm sẵn ở vị trí A. Biết khoản cách từ cọc đến bờ ngang và bờ dọc lần lượt là 6m và 12m. Chọn vị trí hai bờ để lưới giăng cách máy bơm được đặt ở vị trí M một khoản lớn nhất (M là một góc hồ của hình chữ nhật và thuộc khu vực nuôi cá). Khi đó chiều dài của lưới giăng được là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
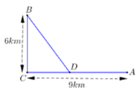
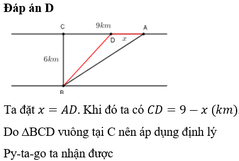
Đặt A D = x → C D = 9 − x suy ra B D = 9 − x 2 + 36 km
Chi phí lắp đặt trên đoạn AD (trên bờ) là T 1 = 100 x triệu đồng
Chi phí lắp đặt trên đoạn DB (dưới nước) là T 2 = 260 9 − x 2 + 36 triệu đồng
Vậy tổng chi phí cần tính là T = T 1 + T 2 = 100 x + 260 9 − x 2 + 36 → f x
Xét hàm số f x = 100 x + 260 x 2 − 18 x + 117 trên đoạn 0 ; 9 → min 0 ; 9 f x = 2340
Dấu = xảy ra khi và chỉ khi x = 13 2 = 6 , 5 km

Đáp án là D.
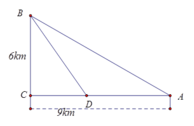
Đặt C D = x , x ∈ 0 ; 9 . Ta có B D = x 2 + 36
Chi phí xây dựng đường ống f x = 100 9 − x + 260 x 2 + 36
Ta có:
f ' x = − 100 + 260 x x 2 + 36 , c h o f ' x = 0 ⇔ 5 x 2 + 36 = 13 x ⇔ x = 5 2
f 0 = 2460 ; f 5 2 = 2340 ; f 9 ≈ 2812 , 33
Chi phí thấp nhất x = 5 2 . Khoảng cách từ A đến D là: 6,5km

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ABC}+59^0+82^0=180^0\)
=>\(\widehat{ABC}=39^0\)
Xét ΔABC có \(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{25}{sin39}=\dfrac{AB}{sin82}\)
=>\(AB=25\cdot\dfrac{sin82}{sin39}\simeq39,34\left(m\right)\)

Đáp án B
Trước tiên ta xác định hàm số f(x) là hàm số tính thời gian người canh hải đăng phải đi.
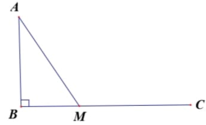
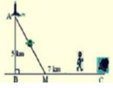
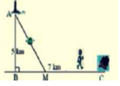
Đặt BM= x , CM =7-x-> A M = x 2 + 25 . Theo đề ta có ngưới canh hải đăng chèo từ A đến M trên bờ biển với v = 4km/h rồi đi bộ đến C với v = 6 km/h
⇒ f ( x ) = x 2 + 25 4 + 7 − x 6 = 3 x 2 + 25 − 2 x + 14 12 với x ∈ ( 0 ; 7 )
f ' ( x ) = 1 12 3 x x 2 + 25 − 2 f ' ( x ) = 0 ⇔ 3 x x 2 + 25 − 2 = 0 ⇔ 3 x − 2 x 2 + 25 = 0 ⇔ 2 x 2 + 25 = 3 x ⇔ 5 x 2 = 100 x ≥ 0 ⇔ x = ± 2 5 x ≥ 0 ⇔ x = 2 5
Vậy đoạn đường ngắn nhất thì giá trị phải nhỏ nhất
f ( 0 ) = 29 12 f ( 2 5 ) = 14 + 5 5 12 f ( 7 ) = 74 4
Vậy giá trị nhỏ nhất của f(x) là 14 + 5 5 12 tại x= 2 5
Nên thời gian đi ít nhât là BM= x = 2 5

Đáp án B
Trước tiên ta xác định hàm số f(x) là hàm số tính thời gian người canh hải đăng phải đi.
Đặt BM= x , CM =7-x ⇒ A M = x 2 + 25 . Theo đề ta có ngưới canh hải đăng chèo từ A đến M trên bờ biển với v = 4km/h rồi đi bộ đến C với v = 6 km/h
⇒ f ( x ) = x 2 + 25 4 + 7 − x 6 = 3 x 2 + 25 − 2 x + 14 12 với x ∈ ( 0 ; 7 )
f ' ( x ) = 1 12 3 x x 2 + 25 − 2 f ' ( x ) = 0 ⇔ 3 x x 2 + 25 − 2 = 0 ⇔ 3 x − 2 x 2 + 25 = 0 ⇔ 2 x 2 + 25 = 3 x ⇔ 5 x 2 = 100 x ≥ 0 ⇔ x = ± 2 5 x ≥ 0 ⇔ x = 2 5
Vậy đoạn đường ngắn nhất thì giá trị phải nhỏ nhất
f ( 0 ) = 29 12 f ( 2 5 ) = 14 + 5 5 12 f ( 7 ) = 74 4
Vậy giá trị nhỏ nhất của f(x) là 14 + 5 5 12 tại x= 2 5
Nên thời gian đi ít nhât là BM= x = 2 5