Cho x,y không âm thỏa mãn x2+y2=1. Tìm giá trị nhỏ nhất P= \(\sqrt{4+5x}+\sqrt{4+5y}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LM
1
LM
13 tháng 5 2017
Ta chứng minh được:
\(0\le x:y\le1\)
\(\Rightarrow x\ge x^2;y\ge y^2;xy\ge0\)
\(P^2=8+5\left(x+y\right)+2\sqrt{16+20\left(x+y\right)+25xy}\)
\(P^2\ge8+5\left(x^2+y^2\right)+2\sqrt{16+20\left(x^2+y^2\right)}\)
\(P^2\ge8+5+2\sqrt{16+20}=25\)
\(\Rightarrow P\ge5\)
Dấu "=" xảy ra \(\Leftrightarrow\orbr{\begin{cases}x=0;y=1\\x=1;y=0\end{cases}}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 12 2021
\(A\le\sqrt{3\left(x+y+y+z+z+x\right)}=\sqrt{6\left(x+y+z\right)}\le\sqrt{6.\sqrt{3\left(x^2+y^2+z^2\right)}}=\sqrt{6\sqrt{3}}\)
\(A_{max}=\sqrt{6\sqrt{3}}\) khi \(x=y=z=\dfrac{1}{\sqrt{3}}\)
Do \(x^2+y^2+z^2=1\Rightarrow0\le x;y;z\le1\)
\(\Rightarrow\left\{{}\begin{matrix}x^2\le x\\y^2\le y\\z^2\le z\end{matrix}\right.\) \(\Rightarrow x+y+z\ge x^2+y^2+z^2=1\)
\(A^2=2\left(x+y+z\right)+2\sqrt{\left(x+y\right)\left(x+z\right)}+2\sqrt{\left(x+y\right)\left(y+z\right)}+2\sqrt{\left(y+z\right)\left(z+x\right)}\)
\(A^2=2\left(x+y+z\right)+2\sqrt{x^2+xy+yz+zx}+2\sqrt{y^2+xy+yz+zx}+2\sqrt{z^2+xy+yz+zx}\)
\(A^2\ge2\left(x+y+z\right)+2\sqrt{x^2}+2\sqrt{y^2}+2\sqrt{z^2}=4\left(x+y+z\right)\ge4\)
\(\Rightarrow A\ge2\)
\(A_{min}=2\) khi \(\left(x;y;z\right)=\left(0;0;1\right)\) và các hoán vị
CM
1 tháng 1 2020
Ta có x + y = 2 ⇒ y = 2 - x ≥ 0 ⇒ 0 ≤ x ≤ 2 . Thay y = 2 - x và biểu thức P ta được
P = 1 3 x 3 + x 2 + 2 - x 2 - x + 1 = 1 3 x 3 + 2 x 2 - 5 x + 5 = f x
với x ∈ 0 ; 2
Đạo hàm f ' x = x 2 + 4 x - 5 = 0 ⇔ x = 1 x = - 5
Do x ∈ 0 ; 2 nên loại x = -5
f 1 = 7 3 ; f 0 = 5 ; f 2 = 17 3
Vậy m i n x ∈ 0 ; 2 P = m i n x ∈ 0 ; 2 f x = 7 3 khi và chỉ khi x = 1
Đáp án B
T
29 tháng 9 2019
Theo em bài này chỉ có min thôi nhé!
Rất tự nhiên để khử căn thức thì ta đặt \(\left(\sqrt{x};\sqrt{y};\sqrt{z}\right)=\left(a;b;c\right)\ge0\)
Khi đó \(M=\frac{a^3}{a^2+ab+b^2}+\frac{b^3}{b^2+bc+c^2}+\frac{c^3}{c^2+ca+a^2}\) với abc = \(\sqrt{xyz}=1\) và a,b,c > 0
Dễ thấy \(\frac{a^3}{a^2+ab+b^2}+\frac{b^3}{b^2+bc+c^2}+\frac{c^3}{c^2+ca+a^2}=\frac{b^3}{a^2+ab+b^2}+\frac{c^3}{b^2+bc+c^2}+\frac{a^3}{c^2+ca+a^2}\)
(chuyển vế qua dùng hằng đẳng thức là xong liền hà)
Do đó \(2M=\frac{a^3+b^3}{a^2+ab+b^2}+\frac{b^3+c^3}{b^2+bc+c^2}+\frac{c^3+a^3}{c^2+ca+a^2}\)
Đến đây thì chứng minh \(\frac{a^3+b^3}{a^2+ab+b^2}\ge\frac{1}{3}\left(a+b\right)\Leftrightarrow\frac{2}{3}\left(a-b\right)^2\left(a+b\right)\ge0\)(đúng)
Áp dụng vào ta thu được: \(2M\ge\frac{2}{3}\left(a+b+c\right)\Rightarrow M\ge\frac{1}{3}\left(a+b+c\right)\ge\sqrt[3]{abc}=1\)
Vậy...
P/s: Ko chắc nha!
CM
29 tháng 4 2018
Chọn C.
Phương pháp:
Đưa biểu thức P về hàm số 1 ẩn x.
Khảo sát, tìm GTNN của hàm số đó.
Cách giải:
DD
Đoàn Đức Hà
Giáo viên
22 tháng 5 2021
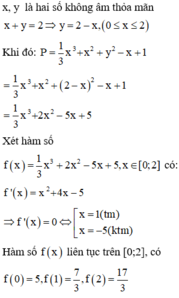
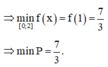
\(P=2x-3\sqrt{xy}+y=2x-3\sqrt{xy}+y+\left(-x-\sqrt{xy}+4y-4\sqrt{y}+16\right)\)
\(=x-4\sqrt{xy}+5y-4\sqrt{y}+16\)
\(=\left(\sqrt{x}-2\sqrt{y}\right)^2+\left(\sqrt{y}-2\right)^2+12\ge12\)
Dấu \(=\)xảy ra khi \(\hept{\begin{cases}\sqrt{x}=2\sqrt{y}\\\sqrt{y}-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=16\\y=4\end{cases}}\).
Với \(x=16,y=4\)thỏa mãn giả thiết.
Vậy \(minP=12\).
CM
5 tháng 7 2018
Đáp án A
P = 1 3 x 3 + x 2 + y 2 − x + 1 = = 1 3 x 3 + x + y 2 − 2 x y − x + 1 = 1 3 x 3 + 4 − 2 x 2 − x − x + 1
⇒ P = 1 3 x 3 + 2 x 2 − 5 x + 5
xét hàm số P x trên 0 ; 2 ta có
P ' = x 2 + 4 x − 5 ⇒ P ' = 0 ⇔ x = 1
Ta tính các giá trị P 0 = 5 ; P 1 = 7 3 ; P 2 = 17 3 ⇒ M i n P = 7 3
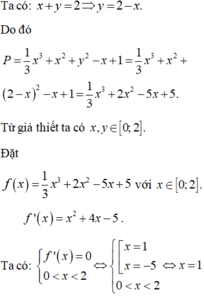
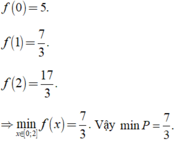
Do \(x^2+y^2=1\Rightarrow0\le x;y\le1\)
\(\Rightarrow\left\{{}\begin{matrix}x^2\le x\\y^2\le y\end{matrix}\right.\) \(\Rightarrow x+y\ge x^2+y^2=1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{4+5x}=a\\\sqrt{4+5y}=b\end{matrix}\right.\) \(\left\{{}\begin{matrix}2\le a;b\le3\\a^2+b^2=8+5\left(x+y\right)\ge13\end{matrix}\right.\)
Do \(2\le a;b\le3\Rightarrow\left\{{}\begin{matrix}\left(a-2\right)\left(a-3\right)\le0\\\left(b-2\right)\left(b-3\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2-5a+6\le0\\b^2-5b+6\le0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a\ge\frac{a^2+6}{5}\\b\ge\frac{b^2+6}{5}\end{matrix}\right.\)
\(\Rightarrow P=a+b\ge\frac{a^2+6}{5}+\frac{b^2+6}{5}=\frac{a^2+b^2+12}{5}\ge\frac{13+12}{5}=5\)
\(\Rightarrow P_{min}=5\) khi \(\left(a;b\right)=\left(2;3\right)\) và hoán vị hay \(\left(x;y\right)=\left(0;1\right)\) và hoán vị
Ủng hộ cách khác
Dễ cm: \(x\ge x^2;y\ge y^2\)
\(P=\sqrt{4+5x}+\sqrt{4+5y}=\sqrt{x+4x+4}+\sqrt{y+4y+4}\ge\sqrt{x^2+4x+4}+\sqrt{y^2+4y+4}=\left|x+2\right|+\left|y+2\right|=x+y+4\ge x^2+y^2+4=1\)"=" khi x;y là hoán vị của (0;1)