Cho tam giác ADE vuông tại A, đường cao AH. Biết AD = 8cm, DE = 17cm
a) Chứng minh tam giác HAE đồng dạng với tam giác HDA
b) Tính HA, HD
c) Gọi M là trung điểm AH, trên tia DA lấy điểm K sao cho A là trung điểm của DK. Chứng minh: tam giác HDK đồng dạng với tam giác MAE
d) Chứng minh: \(\frac{1}{AH^2}=\frac{1}{AD^2}+\frac{1}{AE^2}\) (Không dùng các số đo ở các câu trên)


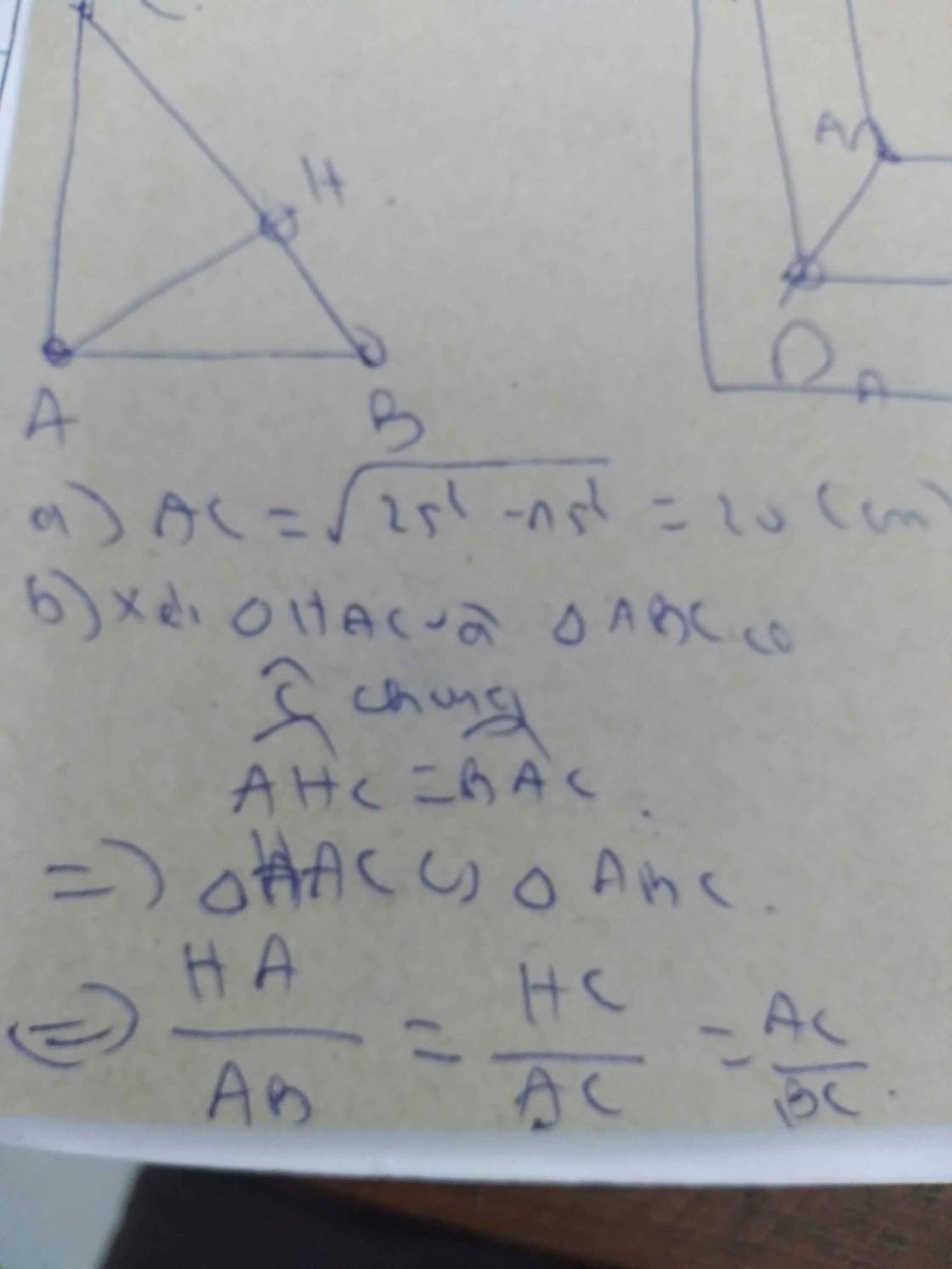

a, tam giác AED vuông tại A (gt)
=> góc E + góc D = 90 (đl)
tam giác AHD vuông tại H => góc HAD + góc D = 90
=> góc HAD = góc E
xét tam giác HAE và tam giác HDA có : góc EAD = góc AHD = 90 do ...
=> tam giác HAE ~ tam giác HDA (g-g)