so sánh A và B biết A=1515+1\1516+1 và B+=1516+1\1517+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. 15 16 v à 155 156
Ta có: 1 - 15 16 = 1 16
1 - 155 156 = 1 156
Mà: 1 16 > 1 156
Nên: 15 16 < 155 156
b. 23 28 v à 24 27
Vì: 23 28 < 24 28
Mà: 24 28 < 24 27
Nên: 23 28 < 24 27



M=338 N=123..1516
=> M có 180 chữ số
=> N có 23 chữ số
=> M>N

a)
9 16 + 8 − 27 + 1 + 7 16 + − 19 27 = 9 16 + 8 − 27 + 1 + 7 16 + − 19 27 = 9 16 + 7 16 + − 8 27 + − 19 27 + 1 = 1 + − 1 + 1 = 1
b)
13 5 + 7 16 − 15 16 − 6 15 = 13 5 + 7 16 − 15 16 + 2 5 = 13 5 + 2 5 + 7 16 − 15 16 = 3 + − 1 2 = 5 2

a)
− 7 31 + 24 19 + 1 15 + 7 31 + − 5 19 = − 7 31 + 7 31 + 24 19 + − 5 19 + 1 15 = 1 + 1 15 = 16 15
b)
15 16 + 13 33 + 1 11 + 7 33 + − 15 16 + 20 66 = 15 16 + 13 33 + 1 11 + 7 33 + − 15 16 + 20 66 = 15 16 + − 15 16 + 13 33 + 7 33 + 1 11 + 20 66 = 20 33 + 13 33 = 1

2:
=1-1+1-1=0
3:
a: =>34*(100+1)/2:a=17
=>a=101
b: =>5/3(x-1/2)=5/4
=>x-1/2=5/4:5/3=3/4
=>x=5/4
1a, \(\dfrac{2005}{2001}\) = 1+\(\dfrac{4}{2001}\); \(\dfrac{2009}{2005}\)=1+\(\dfrac{4}{2005}\)vì\(\dfrac{4}{2001}\)>\(\dfrac{4}{2005}\)nên\(\dfrac{2005}{2001}\)>\(\dfrac{2009}{2005}\)
1b,\(\dfrac{1313}{1515}\)=\(\dfrac{1313:101}{1515:101}\)= \(\dfrac{13}{15}\); \(\dfrac{131313}{151515}\)=\(\dfrac{131313:10101}{151515:10101}\)=\(\dfrac{13}{15}\)
Vậy \(\dfrac{13}{15}\)=\(\dfrac{1313}{1515}\)=\(\dfrac{131313}{151515}\)
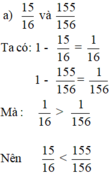
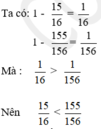
áp dụng tc \(\frac{a}{b}< 1\Rightarrow\frac{a+m}{a+m}< 1\left(m\in N\right)\)
Ta có: \(B=\frac{15^{16}+1}{15^{17}+1}< \frac{15^{16}+1+14}{15^{17}+1+14}\)\(=\frac{15^{16}+15}{15^{17}+15}=\frac{15.\left(15^{15}+1\right)}{15.\left(15^{16}+1\right)}=\frac{15^{15}+1}{15^{16}+1}\)
\(\Rightarrow B< A\)
\(A=\frac{15^{15}+1}{15^{16}+1}\)
\(\Rightarrow15A=\frac{15^{16}+15}{15^{16}+1}\)
\(\Rightarrow15A=\frac{15^{16}+1+14}{15^{16}+1}\)
\(\Rightarrow15A=\frac{15^{16}+1}{15^{16}+1}+\frac{14}{15^{16}+1}\)
\(\Rightarrow15A=1+\frac{14}{15^{16}+1}\)
\(B=\frac{15^{16}+1}{15^{17}+1}\)
\(\Rightarrow15B=\frac{15^{17}+15}{15^{17}+1}\)
\(\Rightarrow15B=\frac{15^{17}+1+14}{15^{17}+1}\)
\(\Rightarrow15B=\frac{15^{17}+1}{15^{17}+1}+\frac{14}{15^{17}+1}\)
\(\Rightarrow15B=1+\frac{14}{15^{17}+1}\)
Vì \(\frac{14}{15^{17}+1}< \frac{14}{15^{16}+1}\) nên \(15B< 15A\)
Vậy B < A