Nhớ ghi cả dkxd ra nha mn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
3
AH
Akai Haruma
Giáo viên
6 tháng 10 2021
a. ĐKXĐ: $x\in\mathbb{R}$
PT \(\Rightarrow \left\{\begin{matrix} 2-x\geq 0\\ x^2+x+2=(3-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ x^2+x+2=x^2-6x+9\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ 7x=7\end{matrix}\right.\Leftrightarrow x=1\)
b. ĐKXĐ: $x\geq -1$
PT $\Leftrightarrow (x^2-1)+\sqrt{x+1}=0$
$\Leftrightarrow (x-1)(x+1)+\sqrt{x+1}=0$
$\Leftrightarrow \sqrt{x+1}[(x-1)\sqrt{x+1}+1]=0$
$\Leftrightarrow \sqrt{x+1}=0$ hoặc $(x-1)\sqrt{x+1}+1=0$
Nếu $\sqrt{x+1}=0$
$\Leftrightarrow x=-1$ (tm)
Nếu $(x-1)\sqrt{x+1}+1=0$
$\Leftrightarrow (x-1)\sqrt{x+1}=-1$
$\Rightarrow (x-1)^2(x+1)=1$
$\Leftrightarrow x^3-x^2-x=0$
$\Leftrightarrow x(x^2-x-1)=0$
$\Leftrightarrow x=0$ hoặc $x^2-x-1=0$
$\Leftrightarrow x=0$ hoặc $x=\frac{1\pm \sqrt{5}}{2}$
Kết hợp đkxđ suy ra $x=0; -1; \frac{1\pm \sqrt{5}}{2}$
AH
Akai Haruma
Giáo viên
6 tháng 10 2021
c. ĐKXĐ: $x\geq 2$
PT $\Leftrightarrow \sqrt{(x-2)(x+2)}-2\sqrt{x-2}=0$
$\Leftrightarrow \sqrt{x-2}(\sqrt{x+2}-2)=0$
$\Leftrightarrow \sqrt{x-2}=0$ hoặc $\sqrt{x+2}-2=0$
$\Leftrightarrow x=2$ (thỏa mãn)
d. ĐKXĐ: $x\geq 3$ hoặc $x\leq -4$
PT \(\Rightarrow \left\{\begin{matrix} 8-x\geq 0\\ x^2+x-12=(8-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 8\\ x^2+x-12=x^2-16x+64\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\leq 8\\ 17x=76\end{matrix}\right.\Leftrightarrow x=\frac{76}{17}\) (tm)
28 tháng 10 2021
1: Ta có: \(\sqrt{3x-5}=2\)
\(\Leftrightarrow3x-5=4\)
hay x=3
2: Ta có: \(\sqrt{25\left(x-1\right)}=20\)
\(\Leftrightarrow x-1=16\)
hay x=17
8 tháng 3 2022
a cách gạch trong phép nhân
b tính kết quả trong ngoặc rồi dùng cách gạch luôn
HT
18 tháng 12 2018
nhấn vào bingbe
ở trên cùng có chữ tài khoản
mình ghi tài khoản của mình trong onljne,vn vào
bên cạnh là mật khẩu
ghi tài khoản của mình trong online.vn vào
rồi nhấn đăng nhập
k ch mình đi
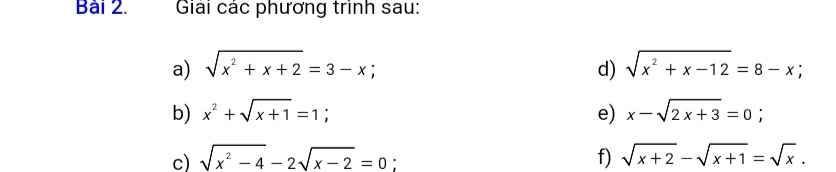
\(a,ĐK:x\le2\\ PT\Leftrightarrow x^2-x-8=4-2x\Leftrightarrow x^2+x-12=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(ktm\right)\\x=-4\left(tm\right)\end{matrix}\right.\Leftrightarrow x=-4\\ b,ĐK:5x^2+10x+1\ge0\\ PT\Leftrightarrow5x^2+10x+1=\left(7-x^2-2x\right)^2\\ \Leftrightarrow5x^2+10x+1=x^4+4x^2+49-14x^2+4x^3-28x\\ \Leftrightarrow x^4+4x^3-15x^2-38x+48=0\\ \Leftrightarrow x^4-x^3+5x^3-5x^2-10x^2+10x-48x+48=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+5x^2-10x-48\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+3x^2+2x^2+6x-16x-48\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+3\right)\left(x^2+2x-16\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\\x^2+2x-16=0\left(1\right)\end{matrix}\right.\)
\(\Delta\left(1\right)=4+64=68\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-2-2\sqrt{17}}{2}=-1-\sqrt{17}\\x=\dfrac{-2+2\sqrt{17}}{2}=-1+\sqrt{17}\end{matrix}\right.\)
Vậy pt có nghiệm ...