tìm gía trị nhỏ nhất \(\text{(3*x^2 -14*x+17)/(x^2 -4*x+4)}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MT
6 tháng 7 2015
x4-x2+7
=(x2)2-2.x2.1/2+1/4+27/4
=(x2-1/4)2+27/4\(\ge\)27/4 ( vì (x2-1/4)2\(\ge\)27/4)
dấu "=" xảy ra khi:
x2-1/4=0
<=>(x-1/2)(x+1/2)=0
<=>x-1/2=0 hoặc x+1/2=0
<=>x=1/2 hoặc x=-1/2
vậy GTNN của x4+x2+7 là 27/4 tại x=1/2 hoặc x=-1/2
CM
6 tháng 2 2018
Đáp án là D.
• Ta có: y , = - 1 - 1 ( 2 + x ) 2 cho y , = 0 ⇔ x = - 1 x = - 3
• Bảng biến thiên:
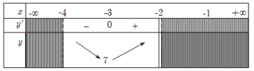
Từ BBT ta có: m i n - 4 ; - 2 y = 7
PL
0
VD
1
1 tháng 3 2015
Để P có giá trị nhỏ nhất thì 14 - x phải = 0. Vậy giá trị nhỏ nhất của P = 0
LT
1
K
4
Nháp trước:
\(A=\frac{3x^2-14x+17}{x^2-4x+4}\left(x\ne2\right)\Leftrightarrow\left(A-3\right)x^2-2\left(2A-7\right)x+\left(4A-17\right)=0\) (1)
Xét A = 3 thì \(2x-5=0\Leftrightarrow x=\frac{5}{2}\)
Xét A khác 3 thì (1) là pt bậc 2 với x là ẩn.(1) có nghiệm tức là:
\(\Delta'=\left(2A-7\right)^2-\left(A-3\right)\left(4A-17\right)\ge0\)
\(\Leftrightarrow4A^2-2.2.7.A+7^2-\left(4A^2-29A+51\right)\ge0\)
\(\Leftrightarrow A-2\ge0\Leftrightarrow A\ge2\)
VẬy..