Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho hình vuông ABCD, M là trung điểm AB. Trên tia đối của tia CB vẽ CN=AM. I là trung điểm MN. Tia DI cắt BC tại E, MN cắt CD tại F. Từ M vẽ MK vuông góc với AB và cắt DE tại K.
a, Cm MKNE là hình thoi (đã làm được)
b, Cm A,I,C thẳng hàng
c, Cho AB=a. Tính diện tích BMEtheo a (Đã làm được)
Giải Giùm mình đi, nhất là câu b
a: Xét ΔADB và ΔADC có
AD chung
DB=DC
AB=AC
=>ΔABD=ΔACD
b: Xét ΔEAK và ΔEBD có
góc EAK=góc EBD
EA=EB
góc AEK=góc BED
=>ΔEAK=ΔEBD
=>AK=BD=CD
c: AK//CD và AK=CD
=>AKDC là hbh
=>KD//AC và AD cắt KC tại trung điểm của mỗi đường
=>F là trung điểm chung của AD và KC
Xét ΔABD có AE/AB=AF/AD
nên EF//BD
=>EF vuông góc AD
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
b: Xét ΔADM vuông tại D và ΔAEM vuông tại E có
AM chung
góc DAM=góc EAM
=>ΔADM=ΔAEM
=>MD=ME
=>ΔMED cân tại M
c: Xét ΔCAB có
M là trung điểm của CB
MF//AB
=>F là trung điểm của AC
a) Xét ΔABH và ΔACH có:
AB=AC (ΔABC cân tại A)
AH là cạnh chung
HB=HC(H là trung điểm của BC)
Nên ΔABH =ΔACH (c.c.c)
=>\(\widehat{AHB}=\widehat{AHC}\)( 2 GÓC TƯƠNG ỨNG)
Ta có: \(\widehat{AHB}+\widehat{AHC}=180^O\)( 2 góc kề bù)
=>\(\widehat{AHB}.2=180^O\Rightarrow\widehat{AHB}=90^O\)
=>AH ⊥ BC
b) Vì ΔABH =ΔACH => \(\widehat{BAH}=\widehat{CAH}\)
Ta có: AD+BD=AB ( D nằm giữa A và B)
AI+IC=AC( I nằm giữa A và C)
Mà AB=AC, BD=IC =>AD=AI
Cho AH và DI cắt nhau tại F
Xét ΔDFA và ΔIFA có:
FA là cạnh chung
\(\widehat{BAH}=\widehat{CAH}\)
AD=AI
Nên ΔDFA=ΔIFA (c.g.c)
=>\(\widehat{DAF}=\widehat{IAF}\)
=>A là tia phân giác của góc DHI
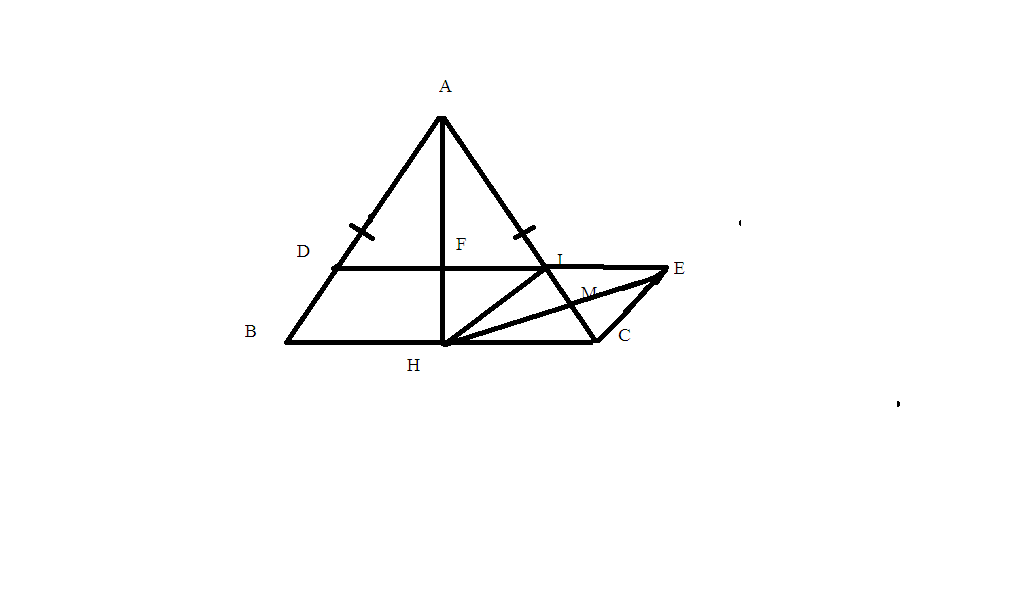
a, +Xét tam giác ABM và AMC có:
AB=AC(Giả thiết)
AM là cạnh chung)
MB=MC(Giả thiết)
=>tam giác ABM=AMC (C-C-C)
b, I là trung điểm của AB (gt) => AI = BI (đn)
DA // BC (gt) => góc DAI = góc IBM (2 góc slt)
xét tam giác DAI và tam giác MBI có : góc DIA = góc BIM (đối đỉnh)
=> tam giác DAI = tam giác MBI (g - c - g)
=> góc IDA = góc IBM
mà góc IBM = góc ACB do tam giác ABC cân tại A (gt)
=> góc ADI = góc ACB
xét tam giác DAM và tam giác CMA có : DM = AC
góc M = góc A (slt)
=> tam giác DAM = tam giác CMA (c - g - c)
=> AD = MC