Các cao nhân giải hộ thần với ạ, đa tạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
1
7 tháng 10 2021
a: Ta có: \(\sqrt{x+2}=3x-4\)
\(\Leftrightarrow9x^2-24x+16-x-2=0\)
\(\Leftrightarrow9x^2-25x+14=0\)
\(\text{Δ}=\left(-25\right)^2-4\cdot9\cdot14=121\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{25-11}{18}=\dfrac{7}{18}\left(loại\right)\\x_2=\dfrac{25+11}{18}=2\left(nhận\right)\end{matrix}\right.\)
20 tháng 6 2023
3:
b: x1^2+x2^2=12
=>(x1+x2)^2-2x1x2=12
=>(2m+2)^2-4m=12
=>4m^2+4m+4=12
=>m^2+m+1=3
=>(m+2)(m-1)=0
=>m=1;m=-2
2:
b: =>|x1|-|x2|=m+3-|-1|=m+2
=>x1^2+x2^2-2|x1x2|=m+2
=>(x1+x2)^2-2x1x2-2|x1x2|=m+2
=>(2m)^2-2(-1)-2|-1|=m+2
=>4m^2-m-2=0
=>m=(1+căn 33)/8; m=(1-căn 33)/8
15 tháng 3 2022
a. \(\widehat{DAB}=\widehat{ABC}=\widehat{BCE}=90^0\)
\(\widehat{ABD}=180^0-\widehat{ABC}-\widehat{EBC}=180^0-60^0-\left(180^0-\widehat{BCE}-\widehat{CEB}\right)=180^0-60^0-\left(180^0-60-\widehat{CEB}\right)=\widehat{CEB}\)\(\Rightarrow\)△ABD∼△CEB (g-g).
\(\Rightarrow\dfrac{AD}{CB}=\dfrac{AB}{CE}\Rightarrow AD.CE=CB.AB\Rightarrow AD.CE=a^2\) không đổi
b. \(\widehat{CAD}=\widehat{BAD}+\widehat{BAC}=60^0+60^0=\widehat{BCE}+\widehat{ACB}=\widehat{ACE}\)
\(\dfrac{AD}{CB}=\dfrac{AB}{CE}\Rightarrow\dfrac{AD}{AC}=\dfrac{AC}{CE}\)
\(\Rightarrow\)△ACD∼△CEA (c-g-c)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ACD}=\widehat{CEA}\\\dfrac{CE}{AC}=\dfrac{EA}{CD}\end{matrix}\right.\)
\(\Rightarrow\)△ACK∼△AEC (g-g).
\(\Rightarrow\dfrac{CK}{EC}=\dfrac{AK}{AC}\Rightarrow\dfrac{CE}{AC}=\dfrac{CK}{AK}\)
\(\Rightarrow\dfrac{AE}{CD}=\dfrac{CK}{AK}\Rightarrow AE.AK=CD.CK\)
DT
2 tháng 3 2022
được thể hiện : qua những phong trào mạnh mẽ kháng chiến đứng lên thể hiện lòng yêu nước nồng nàn , quý báu của dân tộc Việt ta qua nhiều giai đoạn , nhiều thế kỷ vẫn như thế không cho bọn quỷ cướp mảnh đất của mình .
27 tháng 2 2022
\(a,\left(-8,5\right)+16,35+\left(-4,5\right)-\left(-2,25\right)\\ =\left[\left(-8,5\right)+\left(-4,5\right)\right]+\left[16,35-\left(-2,25\right)\right]\\ =-13+18,6=5,6\\ b,5,63+\left(-2,75\right)-\left(-8,94\right)+9,06-15,25\\ =5,63-2,75+8,94+9,06-15,25\)
\(=5,63-\left(2,75+15,25\right)+\left(8,94+9,06\right)\\ =5,63-18+18\\ =5,63\)
27 tháng 2 2022
a) (-8,5) + 16,35 + (-4,5) - (-2,25) = 5,6
b) 5,63 + (-2,75) - (-8,94) + 9,06 - 15,25 = 5,63
CT
5
17 tháng 9 2021
Bài 2 :
Đặt n = abc ( a , b , c là các chữ số ; a ≠ 0 )
Ta có :
abc = 100a + 10b + c mà a = 3c ; b = 2c
=> abc = 300c + 20c + c
=> abc = 321 . c
=> 10 . ab = 320 . c
=> ab = 32 . c
Vì ab là số tự nhiên có 2 chữ số
=> ab < 99 mà ab = 32 . c
=> c < 99 : 32 = \(3\frac{3}{32}\)
Ta xét các trường hợp sau với c là số tự nhiên
+) c = 0 => a = 0 ( loại )
+) c = 1 \(\Rightarrow\hept{\begin{cases}a=3\\b=2\end{cases}}\)
+) c = 2 \(\Rightarrow\hept{\begin{cases}a=6\\b=4\end{cases}}\)
+) c = 3 \(\Rightarrow\hept{\begin{cases}a=9\\b=6\end{cases}}\)
17 tháng 9 2021
Bài 3 :
Với 3 số tự nhiên 0 ; 3 ; 5 viết thành các số có 3 chữ sô
Để 5 nhận giá trị là 50 nên ta đặt số 5 ở vị trí hàng chục
Mà số 0 không thể ở hàng trăm
=> Số 3 ở hàng trăm
Khi đó , ta chỉ viết được 1 số là 350
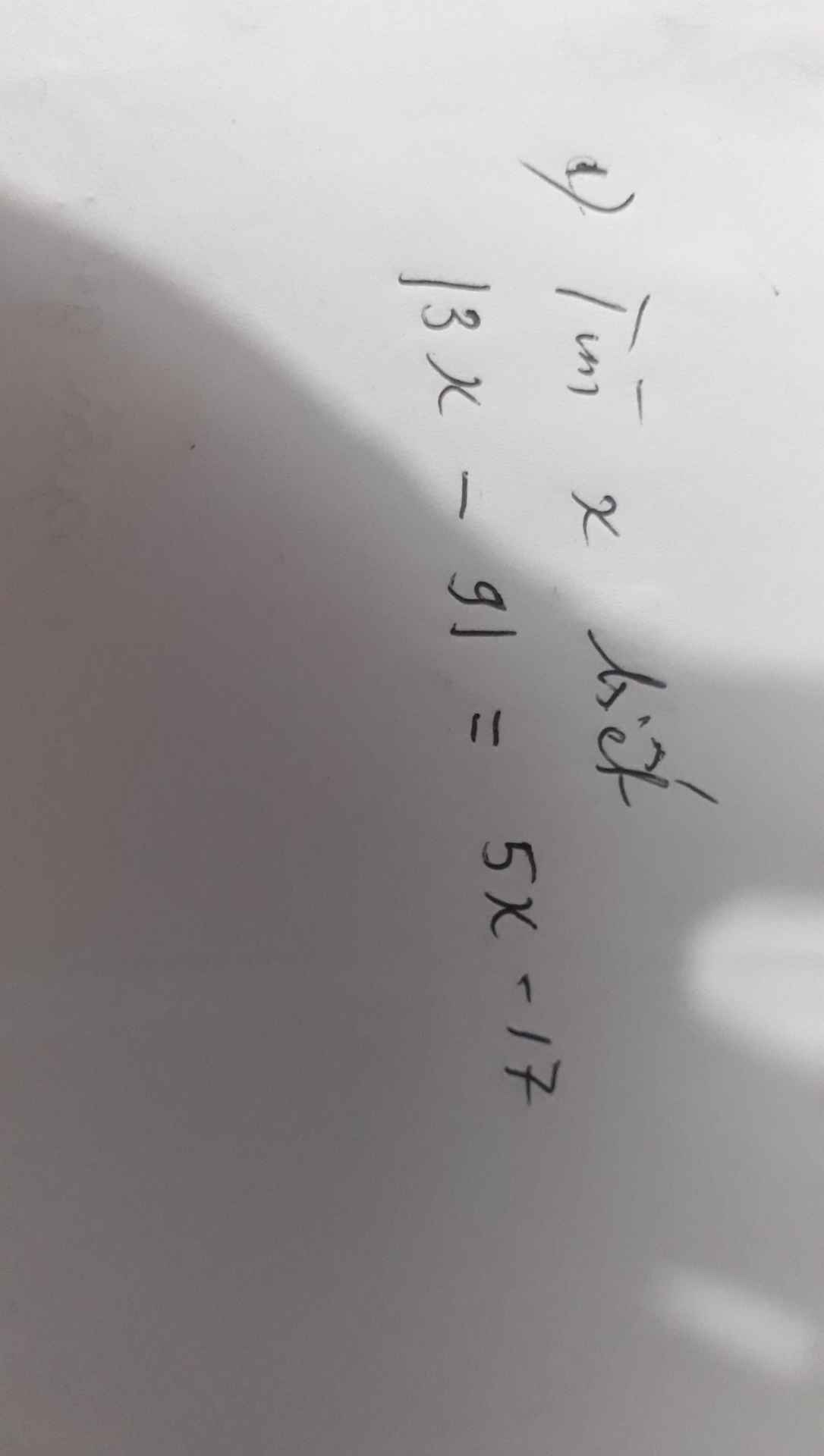
a) ĐKXĐ: x >= 1/2
Pt <=> 2x - 1 = 9
<=> x = 5 (thỏa ĐKXĐ)
b) ĐKXĐ: x>=4/3
Pt <=> 6x - 8 = 4
<=> 6x = 12 <=> x = 2 (thỏa ĐKXĐ)
c) ĐKXĐ: x >= 1
Pt <=> sqrt(x-1)=4
<=> x - 1 = 16 <=> x = 17 (thỏa ĐKXĐ)
Bn dùng \(\sum\) đi nhé