Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=>Qthu1=0,2.340000=68000J\)
\(=>Qthu2=2100.0,2.20=8400J\)
\(=>Qtoa=2.4200.25=210000J\)
\(=>Qthu1+Qthu2< Qtoa\)=>đá nóng chảy hoàn toàn
\(=>0,2.2100.20+0,2.340000+0,2.4200.tcb=2.4200\left(25-tcb\right)\)
\(=>tcb=14,5^oC\)
Cho em hỏi ngu tí ạ vậy tcb ở nhưng phép tính trên vứt đi đâu ạ

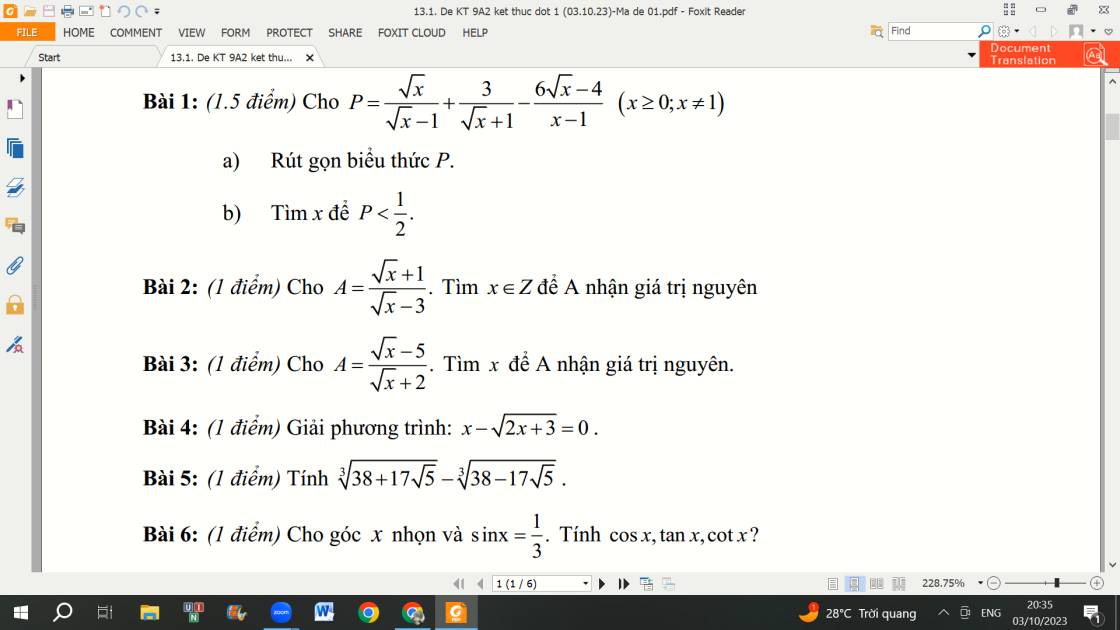
Bài 1:
a: Ta có: \(2\sqrt{75}-\dfrac{1}{5}\sqrt{125}-\dfrac{1}{4}\sqrt{80}+\sqrt{605}\)
\(=6\sqrt{5}-\sqrt{5}-\sqrt{5}+11\sqrt{5}\)
\(=15\sqrt{5}\)
b: ta có: \(\dfrac{3}{\sqrt{2}-1}+\dfrac{3}{\sqrt{2}+1}-\sqrt{\left(4-3\sqrt{2}\right)^2}\)
\(=3\sqrt{2}+3+3\sqrt{2}-3-3\sqrt{2}+4\)
\(=3\sqrt{2}+4\)

Bài 1:
a: \(P=\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}-\dfrac{6\sqrt{x}-4}{x-1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}-\dfrac{6\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)+3\left(\sqrt{x}-1\right)-6\sqrt{x}+4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
b: P<1/2
=>P-1/2<0
=>\(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{1}{2}< 0\)
=>\(\dfrac{2\sqrt{x}-2-\sqrt{x}-1}{2\left(\sqrt{x}+1\right)}< 0\)
=>\(\sqrt{x}-3< 0\)
=>\(\sqrt{x}< 3\)
=>0<=x<9
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0< =x< 9\\x< >1\end{matrix}\right.\)

+ Liên kết chủ đề
+ Liên kết lôgic
- Về hình thức:+ Phép lặp
+ Phép đồng nghĩa, trái nghĩa, liên tưởng
+ Phép nối
+ Phép thế
- Phép liên kết sử dụng trong đoạn: phép thế (Ông - Họa sĩ)

\(\dfrac{x-3}{3}=4-\dfrac{1-2x}{5}\)
=>5(x-3)=60-3(1-2x)
=>5x-15=60-3+6x
=>5x-15=6x+57
=>6x+57=5x-15
hay x=-72(nhận)

\(n_{Fe}=\dfrac{5,6}{56}=0,1\left(mol\right)\\ n_S=\dfrac{0,8}{32}=0,025\left(mol\right)\)
PTHH: Fe + S --to--> FeS
LTL: \(0,1>0,025\rightarrow\) Fe dư
Theo pthh: \(n_{Fe\left(pu\right)}=n_{FeS}=n_S=0,025\left(mol\right)\)
\(\rightarrow\left\{{}\begin{matrix}m_{Fe\left(du\right)}=\left(0,1-0,025\right).56=4,2\left(g\right)\\m_{FeS}=0,025.88=2,2\left(g\right)\end{matrix}\right.\)
PTHH:
Fe + 2HCl ---> FeCl2 + H2
0,075 0,075
FeS + 2HCl ---> FeCl2 + H2S
0,025 0,025
\(\rightarrow\left\{{}\begin{matrix}\%V_{H_2}=\dfrac{0,075}{0,075+0,025}=75\%\\\%V_{H_2S}=100\%-75\%=25\%\end{matrix}\right.\)

- Trích một ít các dd làm mẫu thử, đánh số thứ tự lần lượt
- Cho các dd tác dụng với giấy quỳ tím:
+ QT chuyển đỏ: AgNO3
+ QT chuyển xanh: Na2S, Na2CO3 (1)
+ QT không chuyển màu: K2SO4, KCl (2)
- Cho các dd ở (1) tác dụng với dd HCl dư
+ Có khí mùi trứng thối thoát ra: Na2S
Na2S + 2HCl --> 2NaCl + H2S
+ Có khí không mùi thoát ra: Na2CO3
Na2CO3 + 2HCl --> 2NaCl + CO2 + H2O
- Cho các dd ở (2) tác dụng với dd BaCl2
+ Không hiện tượng: KCl
+ Kết tủa trắng: K2SO4
\(K_2SO_4+BaCl_2\rightarrow BaSO_4\downarrow+2KCl\)


Gọi \(\left\{{}\begin{matrix}n_{Mg}=a\left(mol\right)\\n_{Zn}=b\left(mol\right)\end{matrix}\right.\)
\(n_{H_2}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\\ n_{H_2SO_4}=\dfrac{62.60\%}{98}=0,38\left(mol\right)\)
PTHH:
Mg + H2SO4 ---> MgSO4 + H2
a a a a
Zn + H2SO4 ---. ZnSO4 + H2
b b b b
hệ pt \(\left\{{}\begin{matrix}24a+65b=15,4\\a+b=0,3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0,1\left(mol\right)\\b=0,2\left(mol\right)\end{matrix}\right.\)
\(\rightarrow\left\{{}\begin{matrix}m_{Mg}=0,1.24=2,4\left(g\right)\\m_{Zn}=0,2.65=13\left(g\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\%m_{Mg}=\dfrac{2,4}{15,4}=15,58\%\\\%m_{Zn}=100\%-15,58\%=84,42\%\end{matrix}\right.\)
b, \(\left\{{}\begin{matrix}m_{MgSO_4}=0,1.120=12\left(g\right)\\m_{ZnSO_4}=0,2.161=32,2\left(g\right)\\m_{dd}=62+15,4-0,3.2=76,8\left(g\right)\\m_{H_2SO_4\left(dư\right)}=\left(0,38-0,1-0,2\right).98=7,84\left(g\right)\end{matrix}\right.\)
\(\rightarrow\left\{{}\begin{matrix}C\%_{MgSO_4}=\dfrac{12}{76,8}=15,625\%\\C\%_{ZnSO_4}=\dfrac{32,2}{76,8}=41,2\%\\C\%_{H_2SO_4}=10,2\%\end{matrix}\right.\)








Bằng 2 nha em :)
1+1=2 ngu