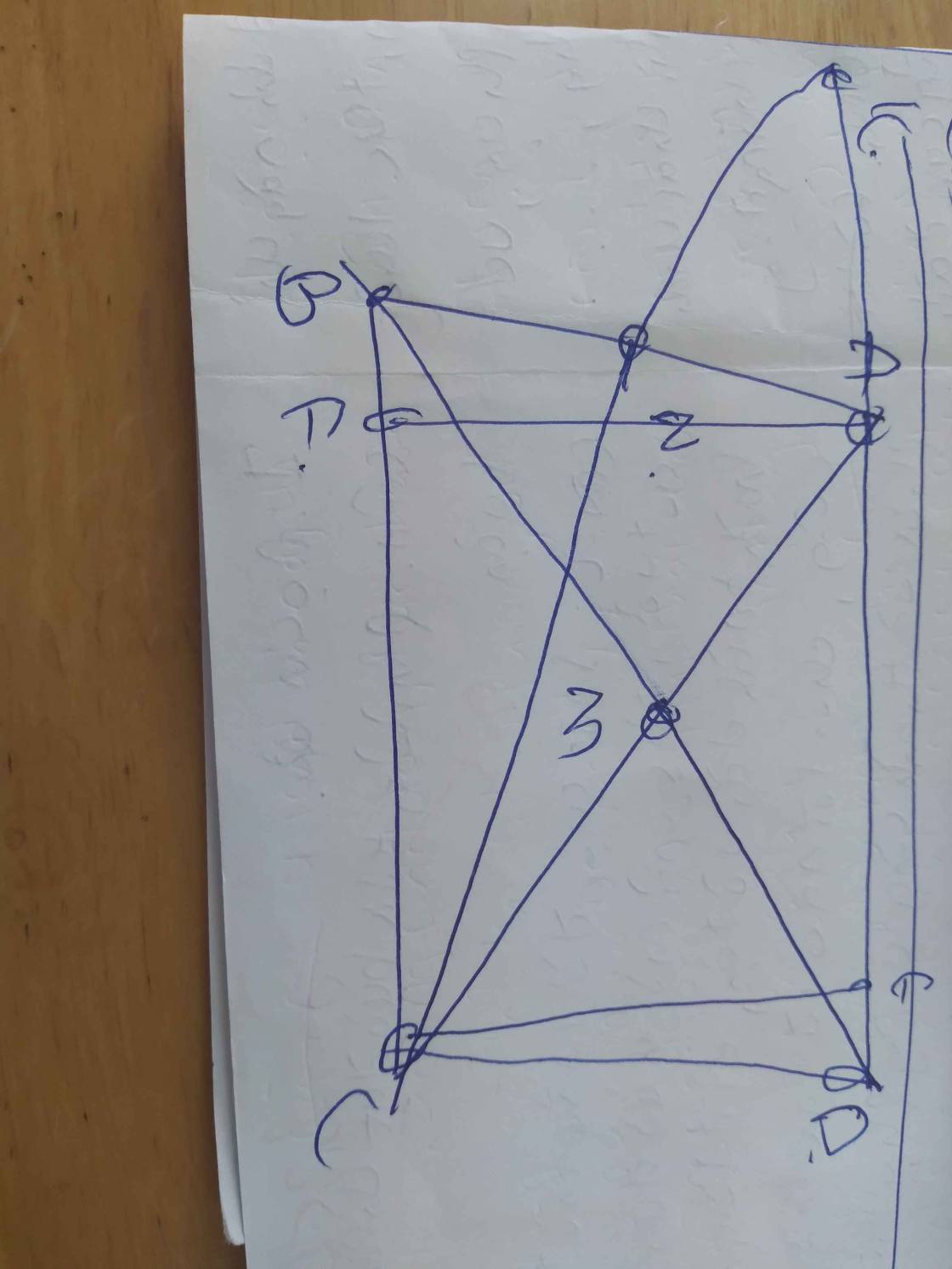
cho tam giác MNPvuong tại M . trên tia đối của MPlay điểm D sao cho MP=MD. trên tia đối củaMN lấy điẻmE sao cho MN=ME. trên tia đối của tia PM lấy điểmK sao cho PK=PD. gọi I là trung điểm của NK . chứng minh 3 điểm E,P,I thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) Xét tam giác MNH và tam giác MKH có:
+ MN = MK (gt).
+ MH chung.
+ NH = KH (H là trung điểm NK).
=> Tam giác MNH = Tam giác MKH (c - c - c).
3) Ta có: MD = MN + ND; ME = MK + KE.
Mà ND = KE (gt); MN = MK (gt).
=> MD = ME.
Xét tam giác MNK có: MN = MK (gt).
=> Tam giác MNK cân tại M.
Mà MH là đường trung tuyến (H là trung điểm NK).
=> MH là đường phân giác \(\widehat{M}\) (Tính chất các đường trong tam giác cân).
Xét tam giác HMD và tam giác HME:
+ MD = ME (cmt).
+ \(\widehat{DMH}=\widehat{EMH}\) (MH là đường phân giác \(\widehat{M}\)).
+ MH chung.
=> Tam giác HMD = Tam giác HME (c - g - c).
4) Xét tam giác MDE có: MD = ME (cmtt).
=> Tam giác MDE cân tại M.
Mà MO là đường trung tuyến (O là trung điểm DE).
=> MO là đường phân giác \(\widehat{M}\) (Tính chất các đường trong tam giác cân).
Mà MH là đường phân giác \(\widehat{M}\) (cmt).
=> Ba điểm M, H, O thẳng hàng.
5) Xét tam giác MDE cân tại M có: MO là đường trung tuyến (O là trung điểm DE).
=> MO là đường cao (Tính chất các đường trong tam giác cân).
=> MO \(\perp\) DE. (1)
Xét tam giác MNK cân tại M có: MH là đường trung tuyến (H là trung điểm NK).
=> MH là đường cao (Tính chất các đường trong tam giác cân).
=> MH \(\perp\) NK
Hay MO \(\perp\) NK. (2)
Từ (1) và (2) => NK // DE (Từ vuông góc đến song song).

UKM THÌ CÓ BÀI TỰA VẬY BẠN SO ĐC CHỨ
a) Xét AIM và BIC có:IA = IB (do I là trung điểm của AB);AIM BIC(hai góc đối đỉnh);IM = IC (giảthiết).Do đó AIM = BIC (c.g.c)Suy ra AM = BC (hai cạnh tương ứng) và MAI CBI(hai góc tương ứng) Mà MAI, CBIlà hai góc ởvịtrí so le trong nên AM // BC.b) Xét ANE và CBE có:EA = EC (do E là trung điểm của AC);AEN CEB(hai góc đối đỉnh);EN= EB(giảthiết).Do đó ANE = CBE (c.g.c)Suy ra NAE BCE(hai góc tương ứng)Mà NAE, BCElà hai góc ởvịtrí so le trong nên AN// BC.c) Ta có AM // BC (theo câu a) và AN // BC (theo câu b)Do đó qua điểm A có hai đường thẳng song song với BC nên theo tiên đềEuclid, hai đường thẳng AM và AN trùng nhau hay ba điểm A, M, N thẳng hàng.Lại có ANE = CBE (theo câu b) nên AN = CB (hai cạnh tương ứng)Mặt khác AM = BC (theo câu a)Do đó AM = AN (cùng bằng BC) Mà ba điểm A, M, N thẳng hàng nên A là trung điểm của MN.a: Xét ΔAMB và ΔCMD có
MA=MC
góc AMB=góc CMD
MB=MD
Do đó: ΔAMB=ΔCMD
b: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
=>AB//CD và AB=CD
c: Xét tứ giác AKBC có
N là trung điểm chung của AB và KC
nên AKBC là hình bình hành
=>AK//BC
mà AD//BC
nên D,A,K thẳng hàng

a. Xét △ABM và △DCM:
\(AM=MD\left(gt\right)\)
\(\hat{AMB}=\hat{DMC}\) (đối đỉnh)
\(BM=MC\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta DCM\left(c.g.c\right)\)
b. Từ a. => \(\hat{MCD}=\hat{MBA}\) (2 góc tương ứng). Mà hai góc này ở vị trí so le trong
\(\Rightarrow CD\text{ // }AB\left(a\right)\)
c. Xét △CIK và △AIB:
\(AI=IC\left(gt\right)\)
\(\hat{AIB}=\hat{CIK}\) (đối đỉnh)
\(BI=IK\left(gt\right)\)
\(\Rightarrow\Delta CIK=\Delta AIB\left(c.g.c\right)\Rightarrow\hat{ICK}=\hat{IAB}\). Mà hai góc ở vị trí so le trong
\(\Rightarrow AB\text{ // }CK\left(b\right)\)
Từ (a) và (b), theo tiên đề Ơ-clit \(\Rightarrow AB\text{ // }DK\)
Vậy: D, C, K thẳng hàng (đpcm).
a) Xét tam giác ABM và tam giác DCM:
BM = CM (M là trung điểm BC).
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh).
MA = MD (cmt).
\(\Rightarrow\) Tam giác ABM = Tam giác DCM (c - g - c).
b) Ta có: \(\widehat{BAM}=\widehat{CDM}\) (Tam giác ABM = Tam giác DCM).
Mà 2 góc này ở vị trí so le trong.
\(\Rightarrow\) CD // AB (dhnb).
c) Xét tứ giác AKCB có:
I là trung điểm AC (gt).
I là trung điểm BK (IB = IK).
\(\Rightarrow\) Tứ giác AKCB là hình bình hành (dhnb).
\(\Rightarrow\) CK // AB (Tính chất hình bình hành).
Mà CD // AB (cmt).
\(\Rightarrow\) D, C, K thẳng hàng.

a: NP=5cm
b: Xét ΔEMD có
EN là đường cao
EN là đường trug tuyến
Do đó: ΔEMD cân tại E

a/
Xét tg AMB và tg MNC có
MB=MC (giả thiết)
MA=MN (giả thiết)
\(\widehat{AMB}=\widehat{NMC}\) (góc đối đỉnh)
=> tg AMB = tg NMC (c.g.c)
b/ Nối A với I cắt BD tại M'
Xét tg ADE có
BE=BA (gt) => DE là trung tuyến của tg ADE
IE=ID (gt) => AI là trung tuyến của tg ADE
=> M' là trọng tâm của tg ADE => \(BM'=\dfrac{1}{3}BD\) (1)
Ta có
MB=MC (gt); MC=CD (gt) => MB=MC=CD
BD=MB+MC+CD
=> \(BM=\dfrac{1}{3}BD\) (2)
Từ (1) và (2) => \(M'\equiv M\)
=> A; M; I thẳng hàng