Cho M =x2 + 2x + 2 | y-1| -1/2
Tìm giá trị nhỏ nhất của M
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Δ=(m+2)^2-4(m^2-1)
=m^2+4m+4-4m^2+4
=-3m^2+4m+8
Để phương trình có hai nghiệm thì -3m^2+4m+8>=0
=>\(\dfrac{2-2\sqrt{7}}{3}< =m< =\dfrac{2+2\sqrt{7}}{3}\)
x1-x2=2
=>(x1-x2)^2=4
=>(x1+x2)^2-4x1x2=4
=>(m+2)^2-4(m^2-1)=4
=>-3m^2+4m+8=4
=>-3m^2+4m+4=0
=>m=2 hoặc m=-2/3

y = x 2 + 2 x + m - 4 = ( x + 1 ) 2 + m - 5
Ta có ( x + 1 ) 2 + m - 5 ∈ m - 5 ; m - 1
Giá trị lớn nhất của hàm số y = x 2 + 2 x + m - 4 trên đoạn[ -2; 1] đạt giá trị nhỏ nhất khi
m - 5 < 0 m - 1 > 0 5 - m = m - 1 ⇔ m = 3
Chọn B.

Chọn đáp án B
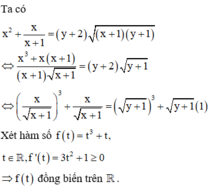
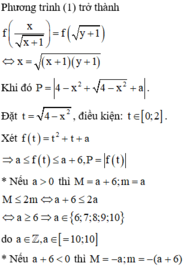
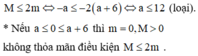
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.

+) \(A=\left(x-3\right)^2+2\)
Vì \(\left(x-3\right)^2\)≥0 ∀x
⇒\(A\)≥2 ∀x
Min A=2⇔\(x=3\)
+) \(B=11-x^2\)
Câu này chỉ tìm được max thôi nha

M=(x^2+2x+1)+2|y-1|-3/2
M=(x+1)^2+2|y-1| -3/2
Vì (x+1)^2>=0 ; 2|y-1|>=0 => M>=-3/2
Dấu = xảy ra <=> x+1=0 và y-1=0<=> x=-1 và y=1
Vậy GTNN M=-3/2 tại x=-1 và y=1
Học tốt
\(M=x^2+2x+2\left|y-1\right|-\frac{1}{2}\)
\(\Rightarrow M=\left(x^2+2.x.1+1^2\right)+2\left|y-1\right|-1-\frac{1}{2}\)(hằng đẳng thức)
\(\Rightarrow M=\left(x+1\right)^2+2\left|y-1\right|-\frac{3}{2}\)
Thấy \(\left|y-1\right|\ge0\forall y\)
\(\Rightarrow2\left|y-1\right|\ge0\forall y\)(1)
Lại thấy: \(\left(x+1\right)^2\ge0\forall x\)(2)
Từ (1)(2)\(\Rightarrow\left(x+1\right)^2+2\left|y+1\right|\ge0\forall x;y\)
\(\Rightarrow\left(x+1\right)^2+2\left|y+1\right|-\frac{3}{2}\ge\frac{-3}{2}\forall x;y\)
hay \(M\ge\frac{-3}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)^2=0\\2\left|y-1\right|=0\end{cases}\Rightarrow\hept{\begin{cases}x+1=0\\\left|y-1\right|=0\end{cases}\Rightarrow}\hept{\begin{cases}x=-1\\y-1=0\end{cases}\Rightarrow}\hept{\begin{cases}x=-1\\y=1\end{cases}}}\)
Khi đó Mmin=\(\frac{-3}{2}\)
Vậy Mmin=\(\frac{-3}{2}\)tại x=-1;y=1