cho tam giác ABC cân tại A, D là trung điểm của BC. Gọi E và F là chân các đường vuông góc kẻ từ D đến AB và AC
a) Chứng minh rằng DE=DF
b) Chứng minh rằng AD là tia phân giác của góc BAC
c) Tính số đo góc ADB
d) cho DB=5cm, AD= 12cm. TÍnh AB
Mọi người giải giúp mình vớiiiiiiiiiiiiiiiiiiii
...
Đọc tiếp
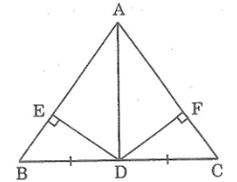
cho tam giác ABC cân tại A, D là trung điểm của BC. Gọi E và F là chân các đường vuông góc kẻ từ D đến AB và AC
a) Chứng minh rằng DE=DF
b) Chứng minh rằng AD là tia phân giác của góc BAC
c) Tính số đo góc ADB
d) cho DB=5cm, AD= 12cm. TÍnh AB
Mọi người giải giúp mình vớiiiiiiiiiiiiiiiiiiii
*Hình:
Giải:
a)Xét T.G EDB và T.G FDC có:
BD=CD(D là trung điểm BC)
^B=^C(GT T.G cân)
^BED=^CFD=90o(GT)
Do đó 2 T.G bằng nhau(CH-GN)
=>DE=DF(2 cạnh tương ứng)(ĐPCM)
b)Xét T.G ABD và T.G ACD có:
AB=AC(GT T.G cân)
BD=CD(D là trung điểm BC)
AD là cạnh chung
Do đó hai T.G bằng nhau(C-C-C)
=>^BAD=^CAD(2 góc tương ứng)
Mà AD nằm trong ^BAC
Nên AD là tia phân giác của ^BAC(ĐPCM)
c)Ta có T.G ABD = T.G ACD (câu b)
=>^ADB=^ADC(2 góc tương ứng)
Mà ^ADB+^ADC=180o(kề bù)
=>^ADB=^ADC=180o/2=90o
Ta có T.G ABD có ^ADB=90o(GT)
=>AB2=AD2+DB2(Đ.Lí PYTAGO)
Hay:AB2=122+52
=>AB2=144+25
=>AB2=169
=>AB=13