Cho tam giác ABC, trên cạnh AB lấy hai điểm D và F sao cho AD=DF=FB. Kẻ DE//FH//BC (E,H thuộc BC) . Biết BC=6, hãy tính độ dài các đoạn thẳng DE, FH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 10 2014
AB=AD+DF+FB
AC=AE+EG+GC
TAM GIÁC ABC=AD+DF+FB+AE+EG+GC
MÀ AD=DF=FB
SUY RA AE=EG=GC
* AD=DF
AE=EG
FD=FB
GE=GC
SUY RA DE ,FG LÀ ĐTB TAM GIÁC ABC
SUY RA DE=1/2 BC
FG=1/2 BC
SUY RA DE+FG=BC
B. DE=FG=1/2BC
SUY RA DE=FG=1/2X9=4.5cm
3 tháng 5 2015
AB=AD+DF+FB
AC=AE+EG+GC
TAM GIÁC ABC=AD+DF+FB+AE+EG+GC
MÀ AD=DF=FB
SUY RA AE=EG=GC
* AD=DF
AE=EG
FD=FB
GE=GC
SUY RA DE ,FG LÀ ĐTB TAM GIÁC ABC
SUY RA DE=1/2 BC
FG=1/2 BC
SUY RA DE+FG=BC
B. DE=FG=1/2BC
SUY RA DE=FG=1/2X9=4.5cm
AM
9 tháng 2 2022
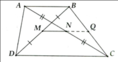
Ta có: \(AD=DE=EF=FB=\dfrac{1}{4}AB\) và \(AM=MN=NP=PC=\dfrac{1}{4}AC\)
Xét \(\Delta ABC\) có: \(\dfrac{AE}{AB}=\dfrac{AN}{AC}=\dfrac{1}{2}\)
\(\Rightarrow EN//BC\) \(\Rightarrow\) EN là đường trung bình của tam giác ABC
\(\Rightarrow EN=\dfrac{BC}{2}=\dfrac{15}{2}=7,5\left(cm\right)\)
Tương tự với tam giác AEN có: \(\dfrac{AD}{AE}=\dfrac{AM}{AN}=\dfrac{1}{2}\)\(\Rightarrow DM//EN\)
\(\Rightarrow\)DM là đường trung bình của tam giác AEN
\(\Rightarrow DM=\dfrac{EN}{2}=\dfrac{7,5}{2}=3,75\left(cm\right)\)
Lại có: \(\dfrac{AE}{AF}=\dfrac{AN}{AP}=\dfrac{2}{3}\)
Áp dụng định lí Ta-let đảo ta có: \(\dfrac{AE}{AF}=\dfrac{AN}{AP}=\dfrac{EN}{FP}=\dfrac{2}{3}\Leftrightarrow\dfrac{7,5}{FP}=\dfrac{2}{3}\Rightarrow FP=11,25cm\)
27 tháng 8 2022
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đo: ΔABD=ΔAED
Suy ra: DB=DE
b:Ta có: AB=AE
DB=DE
Do đó: AD là đường trung trực của BE
CM
6 tháng 2 2018
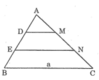
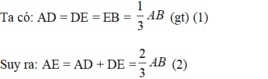
Trong ΔABC, ta có: DM // BC (gt)
Nên 
(Hệ quả định lí Ta-lét)
Suy ra : 
(3)
Từ (1) và (3) suy ra: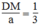 
Suy ra: 
Trong ΔABC, ta có: EN // BC (gt)
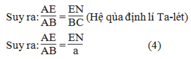
Từ (2) và (4) suy ra: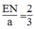 
hay 
LV
11 tháng 2 2020
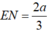
Dựa vào tính chất đường trung bình của tam giác:
DM=EN/2
theo tính chất đương trung bình của hình thang:
EN=(DM+m)/2
14 tháng 2 2022
a: Xét ΔABC có DE//BC
nên AD/AB=AE/AC
=>AE/4=1/3
hay AE=4/3(cm)
b: Xét ΔABC có DE//BC
nên AD/AB=AE/AC
hay \(AD\cdot AC=AE\cdot AB\)
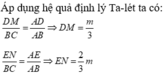
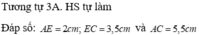
Xét ΔAFH có
DE//FH
Do đó: \(\dfrac{DE}{FH}=\dfrac{AD}{AF}\)
\(\Leftrightarrow FH=2DE\)
Xét hình thang BDEC có
F là trung điểm của BD
FH//ED//BC
Do đó: H là trung điểm của EC
Xét hình thang BDEC có
F là trung điểm của BD
H là trung điểm của EC
Do đó: FH là đường trung bình của hình thang BDEC
Suy ra: \(FH=\dfrac{DE+BC}{2}\)
\(\Leftrightarrow DE=2\left(cm\right)\)
hay FH=4(cm)