Cho tam giác đều ABC có độ dài cạnh bằng a.Trên các cạnh AB và BC lần lượt lấy D và E sao cho AD=BE.Gọi F là giao điểm của AE và CD
a)TÍnh góc AFC
b)C/m tổng FA+FB+FC<2A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 9 2023
Xét ΔCAB có góc CAB=góc CBA
nên ΔCAB cân tại C
=>CA=CB
CE+EA=CA
CD+DB=CB
mà CD=CE và CA=CB
nên EA=DB
Xét ΔEAB và ΔDBA có
EA=DB
góc EAB=góc DBA
BA chung
Do đó: ΔEAB=ΔDBA
=>góc EBA=góc DAB
=>góc FAB=góc FBA
=>FA=FB
2 tháng 6 2023
a: BC=căn 15^2+20^2=25cm
EC=25-5=20cm
ED//AC
=>BD/DA=BE/EC=1/4
=>BD/1=DA/4=15/5=3
=>BD=3cm; DA=12cm
EF//AB
=>FC/FA=EC/EB=4
=>FC/4=FA/1=20/5=4
=>FC=16cm; FA=4cm
b: DE=căn 5^2-3^2=4cm
=>C BDE=3+4+5=12cm
C CEF/C CAB=CE/CB=20/25=4/5
=>C CEF=4/5*(15+20+25)=4/5*60=48cm
16 tháng 4 2022
a: AC=12cm
Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCBD cân tại C
Suy ra: CB=CD
CM
25 tháng 1 2019
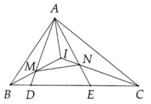
a) Tam giác ABE cân tại B có BI là phân giác nên cũng là đường cao, từ đó B I ⊥ A E . Tương tự C I ⊥ A D .
b) Từ kết quả ý a, chứng minh được I là trực tâm tam giác AMN, từ đó A I ⊥ M N