cho hình chóp SABC có đáy ABC là một tam giác đều cạnh a cạnh SA vuông góc với đáyvà SA = h góc giữa hai mặt pẳng (SBC) và (ABC) bằng600tính khoảng cách từ A đến (SBC) theo a và h
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


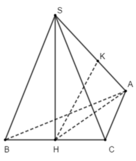
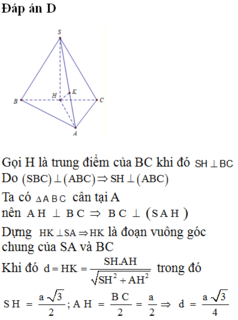
+ Gọi H là trung điểm của BC
Do tam giác ABC cân tại A nên AH ⊥ BC, tam giác SBC đều nên SH ⊥ BC
Mà (SBC) ⊥ (ABC)
Do đó SH ⊥ (ABC)
+ Gọi K là hình chiếu vuông góc của H lên SA ⇒ HK ⊥ SA
Ta có B C ⊥ S H B C ⊥ A H ⇒ B C ⊥ S A H ⇒ B C ⊥ H K
Vậy HK là đoạn vuông góc chung của BC và SA, do đó khoảng cách giữa BC và SA là HK.
+ Tính HK
Tam giác SBC đều cạnh a ⇒ SH = a 3 2
Tam giác ABC vuông cân tại A ⇒ AH = B C 2 = a 2
Tam giác SHA vuông tại H có HK là đường cao ⇒ 1 H K 2 = 1 S H 2 + 1 A H 2
HK = a 3 4
Vậy d(SA; BC) = a 3 4 .
Đáp án C

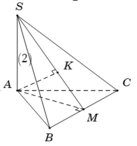
Gọi M là trung điểm BC, suy ra ![]()
Gọi K là hình chiếu của A trên SM suy ra A K ⊥ S M
Từ (1) và (2) suy ra ![]()
Trong
∆
SAM, có 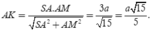
Vậy ![]()
Chọn A.

Nguyễn Khắc Sinh là Nguyen Quang Trung tự hỏi tự trả lời
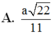
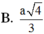
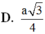

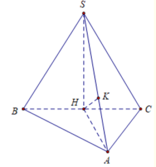


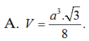
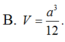

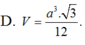
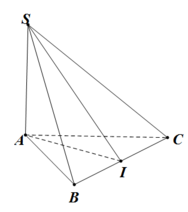


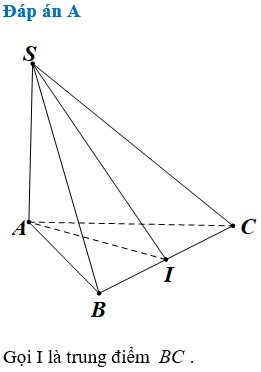
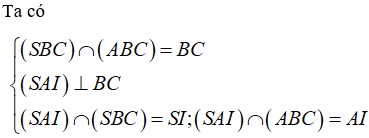
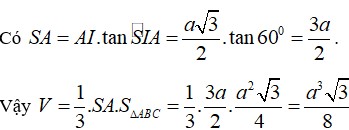
Gọi M là trung điểm BC \(\Rightarrow AM\perp BC\Rightarrow BC\perp\left(SAM\right)\)
\(\Rightarrow\widehat{SMA}=60^0\Rightarrow SA=AM.tan60^0=\frac{a\sqrt{3}}{2}.\sqrt{3}=\frac{3a}{2}\Rightarrow h=\frac{3a}{2}\)
Từ A kẻ \(AH\perp SM\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
Áp dụng hệ thức lượng:
\(\frac{1}{AH^2}=\frac{1}{SA^2}+\frac{1}{AM^2}\Rightarrow AH=\frac{SA.AM}{\sqrt{SA^2+AM^2}}=\frac{3a}{4}\)