Tìm các số nguyên tố a,b,c sao cho abc<ab+bc+ca
Giúp nhanh với, cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
24 tháng 9 2017
Vì a, b, c có vai trũ như nhau nên giả sử a ≤ b ≤ c khi đó
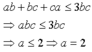
( Vì a là số nguyên tố )
Với a = 2 ta có
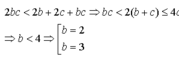
- Nếu b = 2 thì 4c < 2 + 4c thoả món với c là nguyên tố bất kỡ
- Nếu b = 3 thì 6c < 6b + 5c suy ra c < 6 vậy c = 3 hoặc c = 5
Vậy các cạp số (a, b, c) càn Tìm là (2, 2, p) ; (2, 3, 3 ) ; (2, 3, 5 ) và các hoán vị vủa chúng , với p là số nguyên tố .
NK
0
NT
Tìm 3 số tự nhiên a, b, c sao cho cả 3 số abc, ab + bc + ca và a + b + c + 2 đều là các số nguyên tố
0
10 tháng 1 2022
câu 2:
Với p=2→2p+1=5p=2→2p+1=5 không là lập phương 11 số tự nhiên
→p=2→p=2 loại
→p>2→(p,2)=1→p>2→(p,2)=1
Đặt 2p+1=(2k+1)3,k∈N2p+1=(2k+1)3,k∈N vì 2p+12p+1 lẻ
→2p=(2k+1)3−1→2p=(2k+1)3−1
→2p=(2k+1−1)((2k+1)2+(2k+1)+1)→2p=(2k+1−1)((2k+1)2+(2k+1)+1)
→2p=2k(4k2+6k+3)→2p=2k(4k2+6k+3)
→p=k(4k2+6k+3)→p=k(4k2+6k+3)
Vì pp là số nguyên tố, 4k2+6k+3>k4k2+6k+3>k
→k=1→k=1 và 4k2+6k+34k2+6k+3 là số nguyên tố
→4k2+6k+3=13→4k2+6k+3=13 (Khi k=1k=1) là số nguyên tố
→k=1→k=1 chọn
→2p+1=27→2p+1=27
→p=13
câu 3: p−q+2q=(p−q)3→2q=(p−q)((p−q)2−1)=(p−q)(p−q−1)(p−q+1)p−q+2q=(p−q)3→2q=(p−q)((p−q)2−1)=(p−q)(p−q−1)(p−q+1)
Th1: p−qp−q chia hết cho 2 suy ra p−q=2kp−q=2k
Suy ra q=k.(2k−1)(2k+1)q=k.(2k−1)(2k+1)
Do vậy k=1k=1 vì nếu không thì qq thành tích 3 số nguyên lớn hơn 1 suy ra vô lý vì nó là nguyên tố.
Suy ra p−q=2p−q=2 Như vậy q=3,p=5q=3,p=5 Thỏa mãn
TH2: p−q−1p−q−1 chia hết cho 2 suy ra p−q−1=2tp−q−1=2t nên q=(2t+1)t(2t+2)q=(2t+1)t(2t+2)
Do vậy t=0t=0 vì nếu không thì qq thành tích 2 số nguyên lớn hơn 1.
Suy ra p−q−1=0↔p−q=1↔p=3,q=2p−q−1=0↔p−q=1↔p=3,q=2 thay vào đề loại.
TH3: p−q+1=2mp−q+1=2m suy ra q=(2m−1)(2m−2)mq=(2m−1)(2m−2)m
Nếu m≥2m≥2 suy ra qq thành tích 3 số nguyên lớn hơn 1 loại
Suy ra m=0,1m=0,1 thay vào đều loại.
Vậy p=5,q=3p=5,q=3
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1 2022
1.
\(\left(a+b+c\right)^3=a^3+b^3+c^3+3\left(a+b+c\right)\left(ab+bc+ca\right)-3abc\)
Do vế phải chia hết cho 3 \(\Rightarrow\) vế trái chia hết cho 3
\(\Rightarrow a+b+c⋮3\Rightarrow\left(a+b+c\right)^3⋮27\)
\(a+b+c⋮3\Rightarrow3\left(a+b+c\right)⋮9\)
\(\Rightarrow\left(a+b+c\right)^3-\left(a^3+b^3+c^3\right)-3\left(a+b+c\right)\left(ab+bc+ca\right)⋮9\)
\(\Rightarrow3abc⋮9\Rightarrow abc⋮3\)
2.
Đặt \(2p+1=n^3\Rightarrow2p=n^3-1=\left(n-1\right)\left(n^2+n+1\right)\) (hiển nhiên n>1)
Do \(n^2+n+1=n\left(n+1\right)+1\) luôn lẻ \(\Rightarrow n-1\) chẵn \(\Rightarrow n=2k+1\)
\(\Rightarrow2p=\left(2k+1-1\right)\left(n^2+n+1\right)=2k\left(n^2+n+1\right)\)
\(\Rightarrow p=k\left(n^2+n+1\right)\Rightarrow k=1\Rightarrow n=3\)
\(\Rightarrow p=13\)
12 tháng 1 2022
Tham khảo:
2, Với \(p=2->2p+1=5\) không là lập phương 1 số tự nhiên
\(->p=2\) loại
\(-> p>2->(p,2)=1\)
Đặt \(2p+1=(2k+1)^3, k∈ N,\)vì \(2p+1\) lẻ
\(->2p=(2k+1)^3-1\)
\(-> 2p=(2k+1-1)[(2k+1)^2+(2k+1)+1]\)
\(->2p=2k(4k^2+6k+3)\)
\(->p=k(4k^2+6k+3)\)
Vì \(p\) là số nguyên tố, \(4k^2+6k+3>k\)
\(->k=1\) và \(4k^2+6k+3\) là số nguyên tố.
\(->4k^2+6k+3=13(\) khi \(k=1)\) là số nguyên tố
\(->k=1\) (chọn)
\(-> 2p+1=27\)
\(->p=13\)
BG
1
1 tháng 9 2019
Giả sử a≤b≤c⇒ab+bc+ca≤3bca≤b≤c⇒ab+bc+ca≤3bc. Theo giả thiết abc<ab+bc+caabc<ab+bc+ca (1) nên abc<3bc⇒a<3abc<3bc⇒a<3 mà a là số nguyên tố nên a = 2. Thay a = 2 vào (1) được 2bc<2b+2c+bc⇒bc<2(b+c)2bc<2b+2c+bc⇒bc<2(b+c) (2)
Vì b≤c⇒bc<4c⇒b<4b≤c⇒bc<4c⇒b<4. Vì b là số nguyên tố nên b = 2 hoặc b = 3. Với b = 2 thay vào (2) được 2c < 4 + 2c đúng với mọi c là số nguyên tùy ý. Với b = 3 thay vào (2) được c < 6 nên c = 3 hoặc c = 5
Vậy (2; 2; c), (2; 3; 3), (2; 3; 5) với c là số nguyên tố tùy ý
Giả sử a≤b≤c⇒ab+bc+ca≤3bca≤b≤c⇒ab+bc+ca≤3bc. Theo giả thiết abc<ab+bc+caabc<ab+bc+ca (1) nên abc<3bc⇒a<3abc<3bc⇒a<3 mà a là số nguyên tố nên a = 2. Thay a = 2 vào (1) được 2bc<2b+2c+bc⇒bc<2(b+c)2bc<2b+2c+bc⇒bc<2(b+c) (2)
Vì b≤c⇒bc<4c⇒b<4b≤c⇒bc<4c⇒b<4. Vì b là số nguyên tố nên b = 2 hoặc b = 3. Với b = 2 thay vào (2) được 2c < 4 + 2c đúng với mọi c là số nguyên tùy ý. Với b = 3 thay vào (2) được c < 6 nên c = 3 hoặc c = 5
Vậy (2; 2; c), (2; 3; 3), (2; 3; 5) với c là số nguyên tố tùy ý
NP
6
3 tháng 2 2017
Cái này phải có 1 Điều kiện gì đó chứ bạn . Nếu không là 1 đống đấy
VD : a = 1 ; b = 1 ; c = 1
=> 1.1.1 < 1.1 + 1.1 + 1.1
<=> 1 < 3 ( Chọn )
a = 1 ; b = 2 ; c = 3
=> 1.2.3 < 2.3 + 1.2 + 1.3
<=> 6 < 11 (chọn )
NN
1
27 tháng 3 2016
Cách 1 : a4 + b4≥ a3.b + a.b3
Khi và chỉ khi a4 + b4 - a3.b - a.b3 ≥ 0
Khi và chỉ khi a3 (a - b) - b3 (a - b) ≥ 0
Khi và chỉ khi (a - b)(a3 - b3) ≥ 0 khi và chỉ khi (a - b)(a - b)(a2 + ab + b2) ≥ 0
Khi và chỉ khi (a - b)2[(a + b/2)2 + 3.b3/4] ≥ 0 (hiển nhiên đúng với mọi a,b)
Cách 2 : Ta có[ a2 - b2]2 ≥ 0
=> a4 - 2.a2.b2 + b4 ≥ 0
=> a4 + b4 ≥ 2.a2.b2
=> a4 + b4 + a4 + b4 ≥ a4 + b4 + 2.a2.b2
=> 2( a4 + b4) &ge ; ( a2 + b2)2 (1)
Mặt khác (a - b)2≥ 0
=> a2 - 2ab + b2 ≥ 0
=> a2 + b2≥2ab
=> (a2 + b2)( a2 + b2)≥2ab (a2 + b2)
=> (a2 + b2)2 ≥2ab (a2 + b2) (2)
Từ (1) và (2) => 2( a4 + b4 ) ≥ 2ab (a2 + b2)
=> ( a4 + b4 )≥ a3.b + a.b3
Cách 3 :
( a4 + b4 ) -( a3.b + a.b3) = 1/2 (2 a4 + 2 b4 - 2 a3.b -2 a.b3)
= 1/2 [(a4 - 2 a3.b +
Giả sử a≤b≤c⇒ab+bc+ca≤3bca≤b≤c⇒ab+bc+ca≤3bc. Theo giả thiết abc<ab+bc+caabc<ab+bc+ca (1) nên abc<3bc⇒a<3abc<3bc⇒a<3 mà a là số nguyên tố nên a = 2. Thay a = 2 vào (1) được 2bc<2b+2c+bc⇒bc<2(b+c)2bc<2b+2c+bc⇒bc<2(b+c) (2)
Vì b≤c⇒bc<4c⇒b<4b≤c⇒bc<4c⇒b<4. Vì b là số nguyên tố nên b = 2 hoặc b = 3. Với b = 2 thay vào (2) được 2c < 4 + 2c đúng với mọi c là số nguyên tùy ý. Với b = 3 thay vào (2) được c < 6 nên c = 3 hoặc c = 5
Vậy (2; 2; c), (2; 3; 3), (2; 3; 5) với c là số nguyên tố tùy ý
https://diendantoanhoc.net/topic/133814-t%C3%ACm-t%E1%BA%A5t-c%E1%BA%A3-c%C3%A1c-b%E1%BB%99-3-s%E1%BB%91-nguy%C3%AAn-t%E1%BB%91-a-b-c-sao-cho-abc-abbcca/
Link nè bạn