Cho góc xOy= 120o kẻ tia phân giác Ot
1 tính góc tOy
2 Kẻ tia On sao cho tOn=20o tính góc xOn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
9 tháng 4 2016
a)Vì trên cùng một nửa mặt phẳng bờ là đường thẳng xy
Mà xoz=300;zot=800
Suy ra xoz<zot(300<800)
Vậy oz nằm giữa hai tia Ox vàOt
b)Vì oz nằm giữa hai tia Ox vàOt
Suy ra:xoz+zot=zot
Thay số:300+800=zot=1100
Vì trên cùng một nửa mặt phẳng bờ là đường thẳng xy
Mà ot nằm giữa hai hai tia ox và oy
Suy ra:xot+toy=180(kề bù)
1100+toy=1800
toy=1800- 1100=700
c)Vì Om là tia phân giác của góc xoz
Suy ra:xom=moz=xoz:2=300:2=150
Vì On là tia phân giác của góc toy
Suy ra:ton=noy=toy:2=700:2=350
Mà moz+zot+ton=mon
Thay số:150+1100+350=mon=1600
d)Vì theo đề bài kẻ On' sao cho xon'=800
Suy ra:xon'=xom+mon'
800=150+mon'
mon'=650
Ta có:mon'+n'on=mon
650+n'on=mon
Do đó on' ko phải là tia phân giác
9 tháng 4 2016
a) tia Oz nằm giữa 2 tia còn lại
b) ta có: xOz + zOt = xOt
=> 300 + 800 = xOt
=> xOt = 1100
TN
9 tháng 4 2016
a)Vì trên cùng một nửa mặt phẳng bờ là đường thẳng xy
Mà xoz=300;zot=800
Suy ra xoz<zot(300<800)
Vậy oz nằm giữa hai tia Ox vàOt
b)Vì oz nằm giữa hai tia Ox vàOt
Suy ra:xoz+zot=zot
Thay số:300+800=zot=1100
Vì trên cùng một nửa mặt phẳng bờ là đường thẳng xy
Mà ot nằm giữa hai hai tia ox và oy
Suy ra:xot+toy=180(kề bù)
1100+toy=1800
toy=1800- 1100=700
c)Vì Om là tia phân giác của góc xoz
Suy ra:xom=moz=xoz:2=300:2=150
Vì On là tia phân giác của góc toy
Suy ra:ton=noy=toy:2=700:2=350
Mà moz+zot+ton=mon
Thay số:150+1100+350=mon=1600
d)Vì theo đề bài kẻ On' sao cho xon'=800
Suy ra:xon'=xom+mon'
800=150+mon'
mon'=650
Ta có:mon'+n'on=mon
650+n'on=mon
Do đó on' ko phải là tia phân giác
9 tháng 4 2016
b) ta có: xOz + zOt = xOt
=> 300 + 800 = xOt
=> xOt = 1100
CM
12 tháng 12 2017
Hai tam giác vuông ABO (góc B = 90º) và ACO (góc C = 90º) có :
⇒ ΔABO = ΔACO (cạnh huyền – góc nhọn)
⇒ AB = AC (hai cạnh tương ứng) ⇒ ΔABC cân.
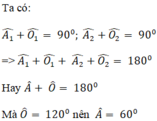
Tam giác cân ABC có góc A = 60º nên là tam giác đều.
29 tháng 1 2021
Ta có: OA là tia phân giác của \(\widehat{xOy}\)(gt)
nên \(\widehat{xOA}=\widehat{yOA}=\dfrac{\widehat{xOy}}{2}=\dfrac{120^0}{2}=60^0\)
hay \(\left\{{}\begin{matrix}\widehat{BOA}=60^0\\\widehat{COA}=60^0\end{matrix}\right.\)
Ta có: ΔAOC vuông tại C(AC\(\perp\)Oy tại C)
nên \(\widehat{CAO}+\widehat{COA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{CAO}=30^0\)
Ta có: ΔAOB vuông tại B(AB\(\perp Ox\) tại B)
nên \(\widehat{BAO}+\widehat{BOA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BAO}=30^0\)
Ta có: \(\widehat{CAB}=\widehat{CAO}+\widehat{BAO}\)(tia AO nằm giữa hai tia AB,AC)
\(\Leftrightarrow\widehat{CAB}=30^0+30^0\)
hay \(\widehat{CAB}=60^0\)
Xét ΔAOC vuông tại C và ΔAOB vuông tại B có
AO chung
\(\widehat{CAO}=\widehat{BAO}\left(=30^0\right)\)
Do đó: ΔAOC=ΔAOB(cạnh huyền-góc nhọn)
hay AC=AB(hai cạnh tương ứng)
Xét ΔABC có AB=AC(cmt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)(cmt)
nên ΔABC đều(Dấu hiệu nhận biết tam giác đều)
1. Vì Ot là tia phân giác của \(\widehat{xOy}\) nên:
\(\widehat{xOt}=\widehat{tOy}=\frac{\widehat{xOy}}{2}=\frac{120^0}{2}=60^0\)
Vậy \(\widehat{tOy}=60^0\)
2. TH1: On nằm giữa Ox và Ot
\(\Rightarrow\widehat{xOn}+\widehat{nOt}=\widehat{xOt}\)
hay \(\widehat{xOn}+20^0=60^0\)
\(\Leftrightarrow\widehat{xOn}=60^0-20^0\)
\(\Leftrightarrow\widehat{xOn}=40^0\)
TH2: Ot nằm giữa Ox và On
\(\Rightarrow\widehat{xOt}+\widehat{tOn}=\widehat{xOn}\)
hay \(60^0+20^0=\widehat{xOn}\)
\(\Leftrightarrow\widehat{xOn}=80^0\)