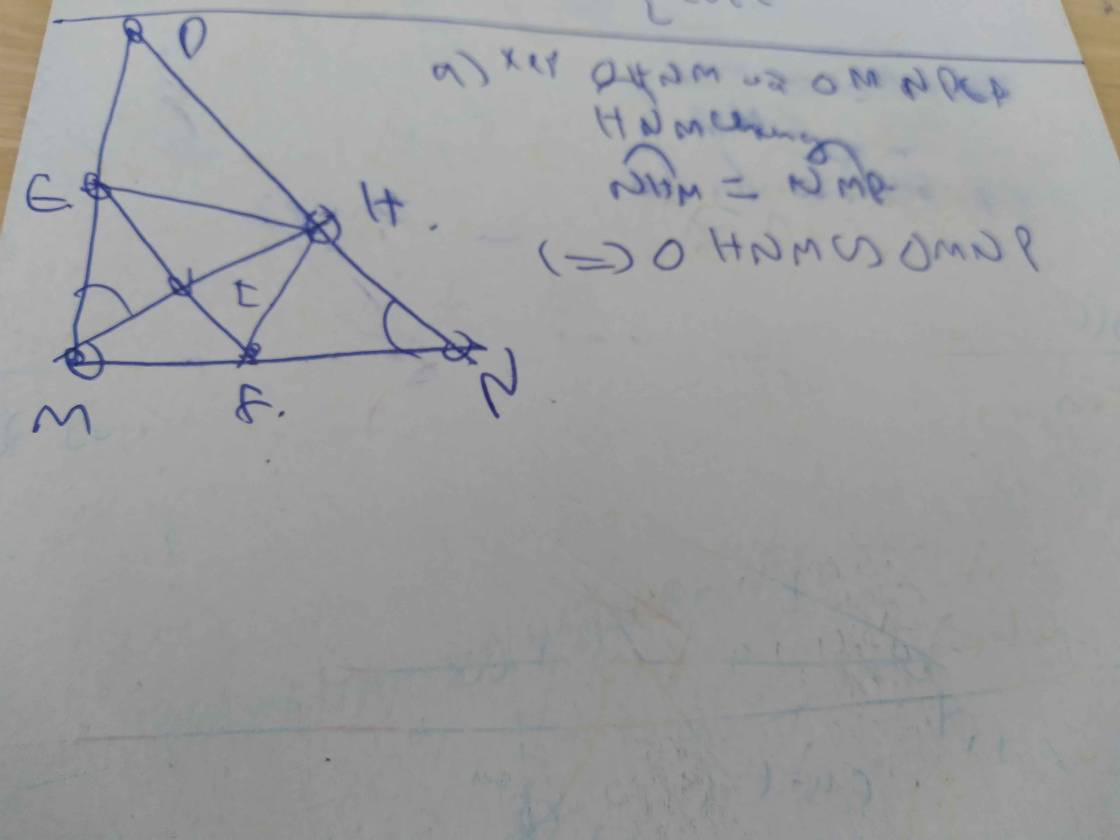
Cho tam giác MNP vuông tại M, đường cao MH
a, Chứng minh rằng: tam giác HNM đồng dạng với tam giác MNP
b, Chứng minh hệ thức: MH2 = NH . PH
c, Lấy điểm E tuỳ ý trên cạnh MP (E ≠ M, E ≠ P), vẽ điểm F trên cạnh MN sao cho góc FHE = 900. Chứng minh rằng: tam giác NFH đồng dạng với tam giác MEH
d, Xác định vị trí của điểm E trên cạnh MP sao cho diện tích tam giác HEF đạt giá trị nhỏ nhất