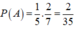Trong một cuộc thi ném bóng rổ, mỗi người được ném bóng 10 lần. Mỗi lần ném bóng vào rổ được 10 điểm, mỗi lần ném bóng ra ngoài bị trừ 4 điểm. Những ai đạt từ 50 điểm trở lên sẽ có thưởng. Theo em, muốn có thưởng phải ném bóng vào rổ ít nhất bao nhiêu lần?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


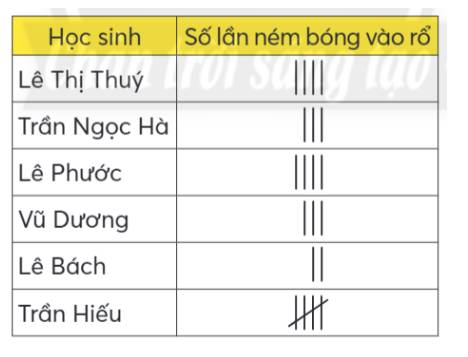
a) Số lần ném bóng vào rổ của mỗi bạn:
Lê Thị Thúy: 4 lần
Trần Ngọc Hà: 3 lần
Lê Phước: 4 lần
Vũ Dương: 3 lần
Lê Bách: 2 lần
Trần Hiếu: 5 lần
Bạn Trần Hiếu ném bóng vào rổ nhiều nhất, Bạn Lê Bách ném bóng vào rổ ít nhất.
b) Trong nhóm học sinh được kiểm tra có 3 bạn đạt yêu cầu.

Tỉ số giữa số bóng ném trúng bóng và số lần được ném bóng của:
-) Nam: \(18:24=\frac{3}{4}\) ( số lần được ném bóng của Nam )
-) An: \(15:20=\frac{3}{4}\) ( số lần được ném bóng của An )
=> Tỉ lệ số lần bóng trúng rổ của hai bạn bằng nhau

Gọi A là biến cố: “Cả hai cùng ném bóng trúng vào rổ. “
Gọi X là biến cố: “người thứ nhất ném trúng rổ. Theo giả thiết P(X)=1/5
Gọi Y là biến cố: “người thứ hai ném trúng rổ.Theo giả thiết P(Y)=2/7
Ta thấy biến cố X, Y là 2 biến cố độc lập nhau, theo công thức nhân xác suất ta có:
![]()
Chọn D.

Gọi A là biến cố: “Cả hai cùng ném bóng trúng vào rổ. “
Gọi X là biến cố: “người thứ nhất ném trúng rổ.“=> P x = 1 5
Gọi Y là biến cố: “người thứ hai ném trúng rổ.“=> P Y = 2 7
Ta thấy biến cố X, Y là 2 biến cố độc lập nhau, theo công thức nhân xác suất ta có:
P(A)=P(X.Y)=P(X).P(Y)= 1 5 . 2 7 = 2 35
Chọn đáp án D

Gọi A là biến cố: “Cả hai cùng ném bóng trúng vào rổ. “
Gọi X là biến cố: “người thứ nhất ném trúng rổ” ⇒ P X = 1 5 .
Gọi Y là biến cố: “người thứ hai ném trúng rổ" ⇒ P Y = 2 7 .
Ta thấy biến cố X, Y là 2 biến cố độc lập nhau, theo công thức nhân xác suất ta có:
P ( A ) = P ( X ) . P ( Y ) = 1 5 . 2 7 = 2 35
Chọn đáp án D