Trong tâp hợp số phức C, giá trị của biểu thức S = 1 + i + i2 + i3 +...+ i2016 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 2 2019
Chọn D.
Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q=i .
Do đó :
CM
27 tháng 3 2019
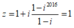
Chọn D.
Ta có : 1 + i + i2 + i3 + ... + i2016 là tổng của cấp số nhân với số hạng đầu u1 = 1, công bội q = i.
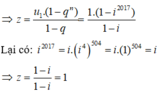
Do đó, phần thực và phần ảo của z lần lượt là: 1 và 0.
CM
25 tháng 1 2017
Chọn B.
Ta có: z = 1 + i2 + i4 +...+ i2n +...+ i2016, n ∈ N
Là tổng của cấp số nhân có 1009 số hạng, số hạng đầu u1 = 1 và công bội q = i nên:
Lại có:
CM
31 tháng 10 2019
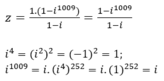
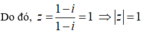
Đáp án B
z = x + y i , ( x , y ∈ ℝ ) ⇒ P = x + 2 2 + y 2 − x 2 - y - 1 2 = 4 x + 2 y + 3 z − 3 − 4 i = 5 ⇔ x - 3 2 + y - 4 2 = 5
Đặt x = 3 + 5 sin t , y = 4 + 5 cost thỏa mãn ( x − 3 ) 2 + ( y − 4 ) 2 = 5
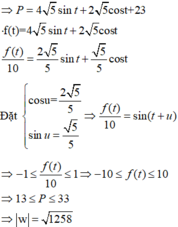
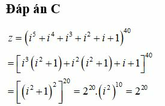
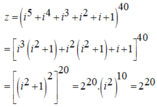
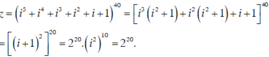
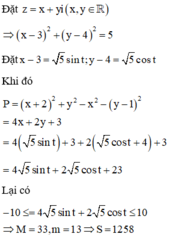
Tổng cấp số nhân với \(u_1=1\); \(u_{2017}=i^{2016}\); \(p=i\)
\(\Rightarrow S=\frac{i^{2017}-1}{i-1}=\frac{i.\left(i^2\right)^{1008}-1}{i-1}=\frac{i-1}{i-1}=1\)