Cho hai đường tròn (O;R) và (O';R') cắt nhau tại A và B (O, O' thuốc hai nửa mặt phẳng bờ AB. Một đường thẳng qua A cắt đường tròn (O) và(O') tương ứng tại C và D ( A nằm giữa C và D). Các tiếp tuyến tại C và D của hai đường tròn cắt nhau tại K. Nối KB cắt CD tại I. Kẻ Ix song song với KD cắt BD tại Ea) CMR tam giác BOO' đồng dạng tam giác BCD (đã làm)b) CM tứ giác BCKD nội tiếp (đã làm)c) CM...
Đọc tiếp
Cho hai đường tròn (O;R) và (O';R') cắt nhau tại A và B (O, O' thuốc hai nửa mặt phẳng bờ AB. Một đường thẳng qua A cắt đường tròn (O) và(O') tương ứng tại C và D ( A nằm giữa C và D). Các tiếp tuyến tại C và D của hai đường tròn cắt nhau tại K. Nối KB cắt CD tại I. Kẻ Ix song song với KD cắt BD tại E
a) CMR tam giác BOO' đồng dạng tam giác BCD (đã làm)
b) CM tứ giác BCKD nội tiếp (đã làm)
c) CM AE là tiếp tuyến của đường tròn (O;R)
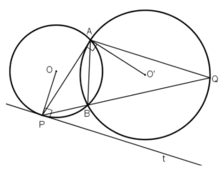
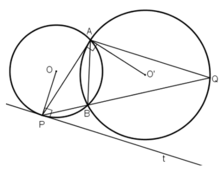
O O' A B C D K I E
Mình sẽ giải lại 2 câu a và b.
a) Vì (O) và (O') giao nhau tại A và B nên AB vuông góc OO'. Do đó ^BO'O = 1/2.^AO'B = ^BDA
Tương tự ^BOO' = ^BCA. Từ đó \(\Delta\)BOO' ~ \(\Delta\)BCD (g.g) (đpcm).
b) Ta thấy: ^KDA = ^ABD (=1/2.Sđ(AD nhỏ của (O')). Tương tự ^KCA= ^ABC
Nên ta có: ^KCB + ^KDB = ^BCD + ^BDC + ^KDA + ^KCA = ^BDC + ^BCD + ^ABD + ^ABC = 1800
Suy ra tứ giác BCKD nội tiếp (đpcm).
c) Vì IE // DK nên ^DIE = ^KDA (So le trong) = ^ABD (cmt) => ^DIE = ^ABE => Tứ giác AIEB nội tiếp
=> ^BAE = ^BIE = ^BKD (Vì IE // KD) = ^BCD (Tứ giác BCKD nt) = 1/2.Sđ(AB nhỏ của (O)
Do vậy AE là tiếp tuyến của (O) (đpcm).
lop 9 kho qua, ve mot nui hinh, chang nhin ra dc hinh nao voi hinh nao