cho hình chữ nhật ABCD ,AB =3 ;BC =4 .M,N là trung điểm của BC và CD .Tính a) độ dài vectoAB +vectoAC +vectoAD b)độ dài vecto AM +vecto AN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
1 tháng 9 2017
Độ dài cạnh BC bằng:
2 × AB = 2 × 12 = 24 (cm)
Chu vi hình chữ nhật ABCD là:
(AB + BC) × 2 = (12 + 24) × 2 = 72 (cm)
Diện tích hình chữ nhật ABCD là:
AB × BC = 12 × 24 = 288 (cm2)
Đáp số: Chu vi: 72cm; Diện tích: 288cm2
29 tháng 1 2024
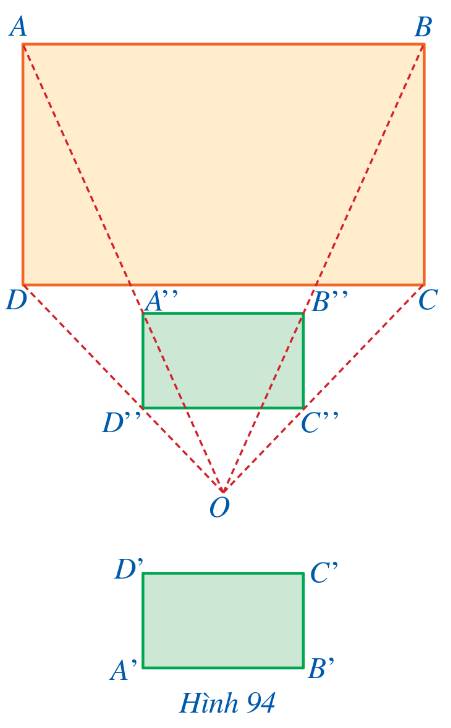
a: Xét ΔODC có D''C''//DC
nên \(\dfrac{D''C''}{DC}=\dfrac{OD''}{OD}=\dfrac{OC''}{OC}=\dfrac{3}{9}=\dfrac{1}{3}\)(1)
Xét ΔOAB có A''B"//AB
nên \(\dfrac{A"B"}{AB}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}=\dfrac{3}{9}=\dfrac{1}{3}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{OD"}{OD}=\dfrac{OC"}{OC}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}\)
mà A"A, B"B, C"C, D"D đều đi qua điểm O
nên hai hình hộp chữ nhật A"B"C"D" và ABCD đồng dạng phối cảnh với nhau
b: ta có: A'B'=C'D'=3cm
A"B"=C"D"=3cm
Do đó: A"B"=C"D"=A'B'=C'D'(3)
ta có: A'D'=B'C'=2cm
A"D"=B"C"=2cm
Do đó: A'D'=B'C'=A"D"=B"C"(4)
Từ (3),(4) suy ra hai hình hộp chữ nhật A"B"C"D" và A'B'C'D' bằng nhau
a: \(\left|\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AC}\right|=2\cdot AC=2\cdot5=10\)
b: \(\left|\overrightarrow{AM}+\overrightarrow{AN}\right|=\left|\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{2}+\dfrac{\overrightarrow{AD}+\overrightarrow{AC}}{2}\right|\)
\(=\left|\dfrac{3\cdot\overrightarrow{AC}}{2}\right|=\dfrac{3}{2}AC=\dfrac{3}{2}\cdot5=\dfrac{15}{2}=7.5\)