4.Cho hàm số f(x) là hàm số chẵn và liên tục trên R thỏa mãn \(\int_{-1}^1f\left(x\right)dx\)=2. Khi đó giá trị tích phân \(\int_0^1f\left(x\right)dx\) là : A.1 B.2 C.\(\frac{1}{4}\) D.\(\frac{1}{2}\)
5.Cho f(x) liên tục trên [0;10] thỏa mãn \(\int_0^{10}f\left(x\right)dx=7\), \(\int_2^6f\left(x\right)dx=3\). Khi đó giá trị của P = \(\int_0^2f\left(x\right)dx+\int_6^{10}f\left(x\right)dx\) có giá trị là: A.1 B.2 C.4 D.3
6.Cho hình phẳng S giới hạn bởi Ox và y =\(\sqrt{1-x^2}\). Thể tích của khối tròn xoay khi quay S quanh Ox là: A.\(\frac{3}{2}\pi\) B.\(\frac{3}{4}\pi\) C.\(\frac{4}{3}\pi\) D.\(\frac{2}{3}\pi\)
7.Tính tích phân I = \(\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\frac{\sin^2x}{\sin3x}dx\) ta được kết quả I = \(\frac{1}{a}ln\left|b+\sqrt{3c}\right|\) với a, b, c \(\in Z\). Giá trị của a + 2b + 3c là: A.5 B.2 C.8 D.3
8.Cho hàm số y = f(x) có đạo hàm f'(x) = \(\frac{1}{2x-1}\), f(1)=1 thì f(5) có giá trị bằng: A.ln2 B.ln2 + 1 C.ln3 D.ln3 + 1



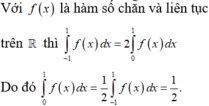
Câu 6:
Hoành độ giao điểm: \(\sqrt{1-x^2}=0\Leftrightarrow x=\pm1\)
\(\Rightarrow V=\pi\int\limits^1_{-1}\left(1-x^2\right)dx=\frac{4}{3}\pi\)
// Hoặc là tư duy theo 1 cách khác, biến đổi pt ban đầu ta có:
\(y=\sqrt{1-x^2}\Leftrightarrow y^2=1-x^2\Leftrightarrow x^2+y^2=1\)
Đây là pt đường tròn tâm O bán kính \(R=1\Rightarrow\) khi quay quanh Ox ta sẽ được một mặt cầu bán kính \(R=1\Rightarrow V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi\)
Câu 7: Về bản chất, đây là 1 con tích phân sai, không thể tính được, do trên miền \(\left[\frac{\pi}{6};\frac{\pi}{2}\right]\) hàm dưới dấu tích phân không xác định tại \(x=\frac{\pi}{3}\) và \(x=\frac{2\pi}{3}\), nhưng nhắm mắt làm ngơ với lỗi ra đề sai đó và ta cứ mặc kệ nó, không quan tâm cứ máy móc áp dụng thì tính như sau:
Biến đổi biểu thức dưới dấu tích phân 1 chút trước:
\(\frac{sin^2x}{sin3x}=\frac{sin^2x}{3sinx-4sin^3x}=\frac{sinx}{3-4sin^2x}=\frac{sinx}{3-4\left(1-cos^2x\right)}=\frac{sinx}{4cos^2x-1}\)
\(\Rightarrow I=\int\limits^{\frac{\pi}{2}}_{\frac{\pi}{6}}\frac{sinx.dx}{4cos^2x-1}\Rightarrow\) đặt \(cosx=t\Rightarrow sinx.dx=-dt\)
\(\Rightarrow I=\int\limits^0_{\frac{\sqrt{3}}{2}}\frac{-dt}{4t^2-1}=\int\limits^{\frac{\sqrt{3}}{2}}_0\frac{dt}{\left(2t-1\right)\left(2t+1\right)}=\frac{1}{2}\int\limits^{\frac{\sqrt{3}}{2}}_0\left(\frac{1}{2t-1}-\frac{1}{2t+1}\right)dt\)
\(I=\frac{1}{4}ln\left|\frac{2t-1}{2t+1}\right|^{\frac{\sqrt{3}}{2}}_0=\frac{1}{4}ln\left(\frac{\sqrt{3}-1}{\sqrt{3}+1}\right)=\frac{1}{4}ln\left(2-\sqrt{3}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}a=4\\b=2\\c=-1\end{matrix}\right.\) \(\Rightarrow a+2b+3c=5\)
Câu 8:
\(f\left(x\right)=\int\frac{1}{2x-1}dx=\frac{1}{2}\int\frac{d\left(2x-1\right)}{2x-1}=\frac{1}{2}ln\left|2x-1\right|+C\)
\(f\left(1\right)=1\Leftrightarrow\frac{1}{2}ln1+C=1\Rightarrow C=1\)
\(\Rightarrow f\left(x\right)=\frac{1}{2}ln\left|2x-1\right|+1\Rightarrow f\left(5\right)=\frac{1}{2}ln9+1=ln3+1\)
Câu 4:
\(I=\int\limits^1_{-1}f\left(x\right)dx=\int\limits^0_{-1}f\left(x\right)dx+\int\limits^1_0f\left(x\right)dx\)
Do \(f\left(x\right)\) là hàm chẵn \(\Rightarrow f\left(x\right)=f\left(-x\right)\) \(\forall x\)
Đặt \(x=-t\Rightarrow dx=-dt;\left\{{}\begin{matrix}x=-1\Rightarrow t=1\\x=0\Rightarrow t=0\end{matrix}\right.\)
\(\Rightarrow\int\limits^0_{-1}f\left(x\right)dx=\int\limits^0_1f\left(t\right).\left(-dt\right)=\int\limits^1_0f\left(t\right)dt=\int\limits^1_0f\left(x\right)dx\)
\(\Rightarrow I=\int\limits^1_0f\left(x\right)dx+\int\limits^1_0f\left(x\right)dx=2\int\limits^1_0f\left(x\right)dx=2\)
\(\Rightarrow\int\limits^1_0f\left(x\right)dx=1\)
Câu 5: Theo tính chất tích phân ta có:
\(\int\limits^{10}_0f\left(x\right)dx=\int\limits^2_0f\left(x\right)dx+\int\limits^6_2f\left(x\right)dx+\int\limits^{10}_6f\left(x\right)dx\)
\(\Rightarrow\int\limits^2_0f\left(x\right)dx+\int\limits^{10}_6f\left(x\right)dx=\int\limits^{10}_0f\left(x\right)dx-\int\limits^6_2f\left(x\right)dx=7-3=4\)