Cho mặt phẳng Oxy cho parabol (P): y=\(\frac{1}{2}x^2\)
a) Vẽ đồ thị (P)
b) Trên (P) lấy điểm A có hoành độ \(x_A\)=-2. Tìm tọa độ điểm M trên trục Õ sao cho \(|MA-MB|\) đạt giá trị lớn nhất, biết rằng B(1;1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

https://h.vn/hoi-dap/question/33566.html
Bạn vào đây xem nhé'
Học tốt!!!!!

a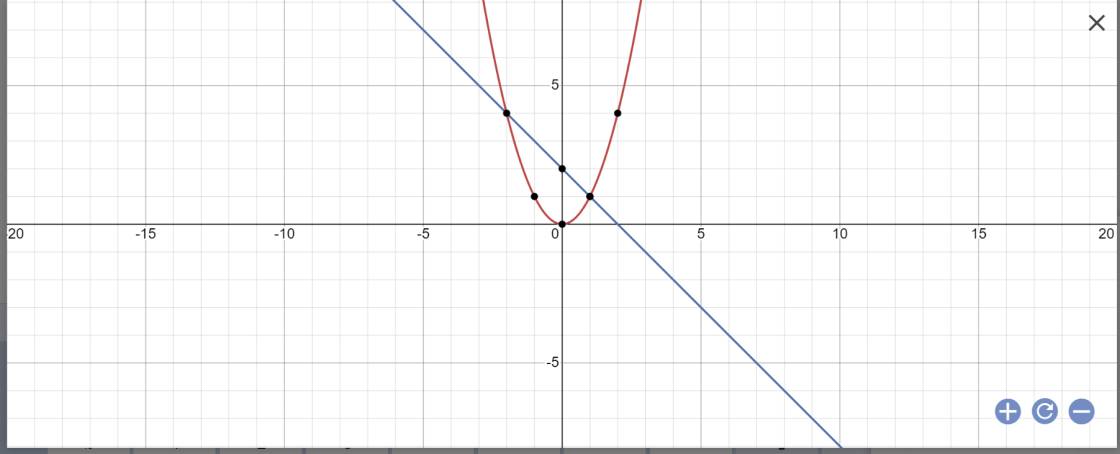
b:
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1
\(A\left(-2;2\right)\)
Áp dụng BĐT tam giác cho tam giác \(MAB\) ta luôn có \(\left|MA-MB\right|\le AB\)
\(\Rightarrow\) \(\left|MA-MB\right|\) đạt GTLN khi M, A, B thẳng hàng \(\Rightarrow\) M là giao điểm của đường thẳng AB và trục Ox
Gọi pt đường thẳng AB có dạng \(y=ax+b\) \(\Rightarrow\left\{{}\begin{matrix}1=a+b\\2=-2a+b\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\frac{-1}{3}\\b=\frac{4}{3}\end{matrix}\right.\) \(\Rightarrow y=-\frac{1}{3}x+\frac{4}{3}\) \(\Rightarrow M\left(4;0\right)\)