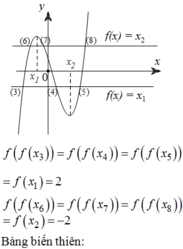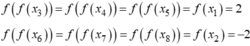Cho hàm số (P): y=x2 và hai điểm A(0

R

RM_7012

23 tháng 3 2019

Cho hàm số (P): y=x2 và hai điểm A(0;1), B(1;3) a. Viết phương trình đường thẳng AB. Tìm toạ độ giao điểm AB với (P) đã cho. b. Viết phương trình đường thẳng d // AB và tiếp xúc (P). c. Viết phương trình đường thẳng d1 ⊥ AB và tiếp xúc (P). d. Chứng tỏ rằng qua điểm A chỉ có duy nhất một đường thẳng cắt (P) tại hai điểm phân biệt C, D sao cho CD=2. Mọi người giúp mình...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 9

0

PD

Phùng Đức Hậu

1 tháng 4 2021

Cho hàm số y= -x² có đồ thị (P) và đường thẳng (d) có hệ số góc k≠0 đi qua điểm I (0;-1).Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt A và B

#Hỏi cộng đồng OLM #Toán lớp 9

1

H

HT2k02

1 tháng 4 2021

Gọi đường thẳng (d) có hàm số y=kx+b (k khác 0) (do hàm số có hệ số góc là k )

Vì (d) đi qua I(0;-1) => -1=0k+b => b=-1

=> y=kx-1(d)

Xét phương trình hoành độ giao điểm chung của (P) và (d) ta có:

-x^2=kx-1

<=> x^2-kx-1=0 (1)

Xét phương trình có a=1;c=-1 => ac=-1 <0

=> (1) luôn có 2 nghiệm phân biệt

=> (P) và (d) luôn cắt nhau tại 2 điểm phân biệt

Đúng(1)

PT

Pham Trong Bach

5 tháng 11 2018

Cho hàm số y = f x = a x 3 + b x 2 + c x + d có hai cực trị x 1 , x 2 thỏa mãn - 2 < x 1 < 0 < x ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

5 tháng 11 2018

Đáp án D.

Đúng(0)

PT

Pham Trong Bach

11 tháng 12 2018

Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d có hai cực trị x 1 , x 2 thỏa - 2 < x 1 < 0 < x 2 ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

11 tháng 12 2018

Suy ra số điểm cực tiểu của hàm số là 4

Đúng(0)

PT

Pham Trong Bach

22 tháng 11 2018

Cho đồ thị hàm số y = x 2 và y = 3 x 2 . Tìm giao điểm của hai đồ thị hàm số đã cho?

A. O(0; 0)

B. A(1; 1)

C. O(0; 0) và A(1; 1)

D. O(0; 0) và B( 1; 3)

#Hỏi cộng đồng OLM #Toán lớp 9

1

CM

Cao Minh Tâm

22 tháng 11 2018

Đáp án A

Hoành độ giao điểm của hai đồ thị hàm số đã cho là nghiệm phương trình:

x2 = 3x2 ⇔ -2x2 = 0 ⇔ x = 0

Với x = 0 thì y= 02 = 0

Do đó,đồ thị hai hàm số đã cho cắt nhau tại điểm duy nhất là gốc tọa độ O(0; 0).

Đúng(0)

MC

Minh Châu

9 tháng 5 2022

Bài 1 Giải các phương trình sau: a) x2 + 6x + 8 = 0 b) 9x2 – 6x + 1 = 0Bài 2. Cho hai hàm số y = 2x2 và y = x + 1a) Vẽ đồ thì hai hàm số này trên cùng một mặt phẳng tọa độ.b) Tìm tọa độ giao điểm của hai đồ thị đó.Bài 3 : Cho phương trình x2 + 2x + 2m = 0 a) Tìm m để phương trình có hai nghiệm trái dấu.b) Tìm m để phương trình có...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 9

2

NL

Nguyễn Lê Phước Thịnh

9 tháng 5 2022

Bài 1:

a: \(x^2+6x+8=0\)

=>(x+2)(x+4)=0

=>x=-2 hoặc x=-4

b: \(9x^2-6x+1=0\)

=>(3x-1)²=0

=>3x-1=0

hay x=1/3

Đúng(2)

HP

hưng phúc

9 tháng 5 2022

Câu 1:

a. x²+ 6x + 8 = 0

\(\Delta'=3^2-8=1>0\)

Do \(\Delta'>0\) nên phương trình có 2 nghiệm phân biệt:

\(x_1=\dfrac{-3+\sqrt{1}}{1}=-2\)

\(x_2=\dfrac{-3-\sqrt{1}}{1}=-4\)

b. 9x² - 6x + 1 = 0

\(\Delta'=\left(-3\right)^2-9.1=0=0\)

Do \(\Delta'=0\) nên phương trình có nghiệm kép:

\(x_1=x_2=\dfrac{3}{9}=\dfrac{1}{3}\)

Đúng(1)

NT

nguyễn thảo hân

18 tháng 7 2019 - olm

cho hàm số y=x2-5x+8 có đồ thị là (P) và hai điểm A(4,-1) , B(10,5) . biết điểm M(x0,y0) trên (P) thỏa mãn diện tích tam giác MAB nhỏ nhất . tính tổng x₀ + y₀

#Hỏi cộng đồng OLM #Toán lớp 10

0

H

hằng

15 tháng 4 2021

cho hai hàm số y=x² và y=2x-m+2

a) tìm m để đồ thị hai hàm số trên chỉ có một điểm chung ? tìm tọa độ điểm chung đó ?

b) tìm m để đồ thị hai hàm số trên cắt nhau tại hai điểm điểm phân biệt có hoành độ lần lượt là x₁,x₂ sao cho x₁² - x₁x₂ +7x₂=5

#Hỏi cộng đồng OLM #Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

15 tháng 4 2021

a) Phương trình hoành độ giao điểm là:

\(x^2=2x-m+2\)

\(\Leftrightarrow x^2-2x+m-2=0\)

Để hai đồ thị hàm số chỉ có một điểm chung thì Δ=0

\(\Leftrightarrow4-1\cdot\left(m-2\right)=0\)

\(\Leftrightarrow m-2=4\)

hay m=6

Đúng(0)

MN

Minh Nguyệt

14 tháng 12 2020

Cho hàm số y = f(x) = ax⁴ + bx³ + cx² + dx + e (a≠0) có đồ thị (C) cắt trục hoành tại bốn điểm phân biệt là A(x1; 0), B(x2 ; 0), C(x3 ; 0), D(x4;0), với x1, x2, x3, x4 theo thứ tự lập thành cấp số cộng và hai tiếp tuyến của (C) tại A, B vuông góc với nhau. Tính giá trị của biếu thức S = (f ' (x3) + f ' (x4))²⁰²⁰

#Hỏi cộng đồng OLM #Toán lớp 11

3

NV

Nguyễn Việt Lâm

Giáo viên

14 tháng 12 2020

Do \(f\left(x\right)=ax^4+bx^3+cx^2+dx+e\) có 4 nghiệm pb \(x_1;x_2;x_3;x_4\)

\(\Rightarrow f\left(x\right)=a\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)\)

Ta có:

\(f'\left(x\right)=a\left[\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)+\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)+\left(x-x_1\right)\left(x-x_3\right)\left(x-x_4\right)+\left(x-x_1\right)\left(x-x_2\right)\left(x-x_4\right)\right]\)

\(\Rightarrow\left\{{}\begin{matrix}f'\left(x_1\right)=a\left(x_1-x_2\right)\left(x_1-x_3\right)\left(x_1-x_4\right)\\f'\left(x_2\right)=a\left(x_2-x_1\right)\left(x_2-x_3\right)\left(x_2-x_4\right)\\f'\left(x_3\right)=a\left(x_3-x_1\right)\left(x_3-x_2\right)\left(x_3-x_4\right)\\f'\left(x_4\right)=a\left(x_4-x_1\right)\left(x_4-x_2\right)\left(x_4-x_3\right)\end{matrix}\right.\)

Mà tiếp tuyến tại A và B vuông góc \(\Leftrightarrow f'\left(x_1\right).f'\left(x_2\right)=-1\) (1)

Do \(x_1;x_2;x_3;x_4\) lập thành 1 CSC, giả sử công sai của CSC là \(d\)

\(\Rightarrow\left\{{}\begin{matrix}x_2=x_1+d\\x_3=x_1+2d\\x_4=x_1+3d\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}f'\left(x_1\right)=a.\left(-d\right).\left(-2d\right).\left(-3d\right)=-6ad^3\\f'\left(x_2\right)=a.d.\left(-d\right).\left(-2d\right)=2ad^3\\f'\left(x_3\right)=a.2d.d.\left(-d\right)=-2ad^3\\f'\left(x_4\right)=a.3d.2d.d=6ad^3\end{matrix}\right.\)

Thế vào (1): \(-12a^2d^6=-1\Leftrightarrow12a^2d^6=1\)

\(\Rightarrow f'\left(x_3\right)+f'\left(x_4\right)=4ad^3\)

\(\Rightarrow S=\left(4ad^3\right)^{2020}=\left(16a^2d^6\right)^{1010}=\left(\dfrac{4}{3}.12a^2d^6\right)^{1010}=\left(\dfrac{4}{3}\right)^{1010}\)

Bài gì mà dễ sợ :(

Đúng(1)

MN

Minh Nguyệt

14 tháng 12 2020

undefined