Cho tg ABC , hai đường trung trực của 2 cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. CM rằng :
a) D là trung điểm của cạnh BC
b) Số đó góc A bằng tổng số đo góc B và C
Help Me
Giúp mình đi mik k nhiều nhất có thể luôn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 4 2018
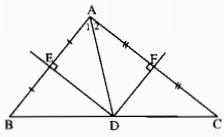
a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b) Ta có: Tam giác DEA = tam giác DEA (c.g.c) nên góc B = góc A1
<=> góc C = góc A2
=> Góc A = góc A1 + góc A2 = góc B + góc C.
23 tháng 7 2021
a) Ta có: M nằm trên đường trung trực của AB(gt)
nên MA=MB(1)
Ta có: M nằm trên đường trung trực của AC(gt)\
nên MA=MC(2)
Từ (1) và (2) suy ra MB=MC
hay M là trung điểm của BC(đpcm)
CM
8 tháng 5 2018
Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
a) mik cm đc ý a thôi
a,tự vẽ hình ra nha!
Trên nửa mặt phẳng bờ BC ko chứa điểm A kẻ CH vug góc DH tại H sao cho DA=DH
Xét \(\Delta ABD\)và \(\Delta HBC\)có:
\(\widehat{A_1}=\widehat{H_1}\left(DA\perp AB,HD\perp HC\right)\)
DH=DA(theo cách vẽ)
\(\widehat{D_1}=\widehat{D_2}\)(đối đỉnh)
=> tam giác ABD= tam giác HCD(ch-gn)
=>DB=DC(2 cạnh t/ư)
=> D lak trung điểm của BC(đpcm)