Tìm các số nguyên x,y sao cho: 2xy+y=10x+17
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 4 2017
Ta có :
\(2xy+y=10x+17\) \(\left(x,y\in Z\right)\)
\(2xy+y-10x=17\)
\(y\left(2x+1\right)-5.2x=17\)
\(y\left(2x+1\right)-5.2x-5=17-5\)
\(y\left(2x+1\right)-5\left(2x+1\right)=12\)
\(\left(2x+1\right)\left(y-5\right)=12\)
Vì \(x,y\in Z\Rightarrow2x+1;y-5\in Z\) và \(2x+1⋮̸\) \(2\)
\(2x+1;y-5\inƯ\left(12\right)\)
Ta có bảng :
| \(x\) | \(2x+1\) | \(y-5\) | \(y\) | \(Đk\) \(x,y\in Z\) |
| \(0\) | \(1\) | \(12\) | \(17\) | \(TM\) |
| \(1\) | \(3\) | \(4\) | \(9\) | \(TM\) |
| \(-1\) | \(-1\) | \(-12\) | \(-7\) | \(TM\) |
| \(-2\) | \(-3\) | \(-4\) | \(1\) | \(TM\) |
Vậy cặp giá trị \(\left(x,y\right)\) cần tìm là : \(\left(0,17\right);\left(1,9\right);\left(-1;-7\right);\left(-2,1\right)\)
~Chúc bn học tốt ~
9 tháng 4 2017
2xy+y=10x+17
\(\Leftrightarrow\)2xy+y-10x-17=0
\(\Leftrightarrow\)y.(2x+1)-5(2x+1)=12
\(\Leftrightarrow\) ( 2x+1).(y-5)=12
2x+1; y-5 là ước của 12
ta thấy 2x +1 luôn là số lẻ.
ta có
| 2x+1 | 1 | 3 | -3 | 1 | |
| y-4 | 4 | 12 | -4 | -12 |
ta giải theo phương trình rồi tìm x;y
MN
2
28 tháng 12 2017
\(2xy-10x+y=17\Leftrightarrow2xy-10x+y-5=12\Leftrightarrow.\)\(\Leftrightarrow2x\left(y-5\right)+\left(y-5\right)=12\Leftrightarrow\left(y-5\right)\left(2x+1\right)=12.\)\(đk:.y>6\)
- Ta phân tích số 12 thành tích của hai số, lưu ý khi x là số tự nhiên thì 2x + 1 là một số lẻ. Và dĩ nhiên khi đó (y - 5) là số chẵn.
Có hai trường hợp sau :
-Trường hợp 1: \(\hept{\begin{cases}2x+1=1\\y-6=12\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=18\end{cases}}}\)
-Trường hợp 2: \(\hept{\begin{cases}2x+1=3\\y-6=4\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=10\end{cases}}}\)
Trả lời x = 0 , y = 18 và x = 1 , y = 10
30 tháng 12 2017
Xin đính chính lại : (Cháu đánh máy nhầm 5 thành 6 - thành thật xin lỗi mọi người)
.....Có hai trường hợp xẩy ra :
- Trường hợp 1 : \(\hept{\begin{cases}2x+1=1\\y-5=12\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=17\end{cases}}}\)
- Trường hợp 2 : \(\hept{\begin{cases}2x+1=3\\y-5=4\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=9\end{cases}}}\)
Trả lời : x = 0 , y = 17 và x = 1 , y = 9
6 tháng 12 2018
\(2xy-10x+y=17\)
\(\Leftrightarrow2x\left(y-5\right)+\left(y-5\right)=12\)
\(\Leftrightarrow\left(2x+1\right)\left(y-5\right)=12\)
Vì x \(\in\) N nên 2x + 1 là ước lẻ của 12 \(\Rightarrow2x+1\in\left\{1;3\right\}\)
Ta có bảng sau:
| 2x + 1 | 1 | 3 |
| y - 5 | 12 | 4 |
| x | 0 | 1 |
| y | 17 | 9 |
NM
1
26 tháng 5 2022
\(2xy-x-y=3\Leftrightarrow x\left(2y-1\right)-y=3\Leftrightarrow-2x\left(2y-1\right)+2y=-6\Leftrightarrow-2x\left(2y-1\right)+2y-1=-7\Leftrightarrow\left(1-2x\right)\left(2y-1\right)=-7\)Đến đây do x,y nguyên nên bạn lập bảng để tìm ra x,y nhá
MP
1
11 tháng 12 2021
\(\Rightarrow2x-4xy+2y=0\\ \Rightarrow2x\left(1-2y\right)+2y-1=-1\\ \Rightarrow2x\left(1-2y\right)-\left(1-2y\right)=-1\\ \Rightarrow\left(2x-1\right)\left(2y-1\right)=1=1.1=\left(-1\right)\left(-1\right)\)
Với \(\left\{{}\begin{matrix}2x-1=1\\2y-1=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\rightarrow\left(1;1\right)\)
Với \(\left\{{}\begin{matrix}2x-1=-1\\2y-1=-1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\rightarrow\left(0;0\right)\)
Vậy các cặp \(\left(x;y\right)\) cần tìm là \(\left(1;1\right);\left(0;0\right)\)
LN
0
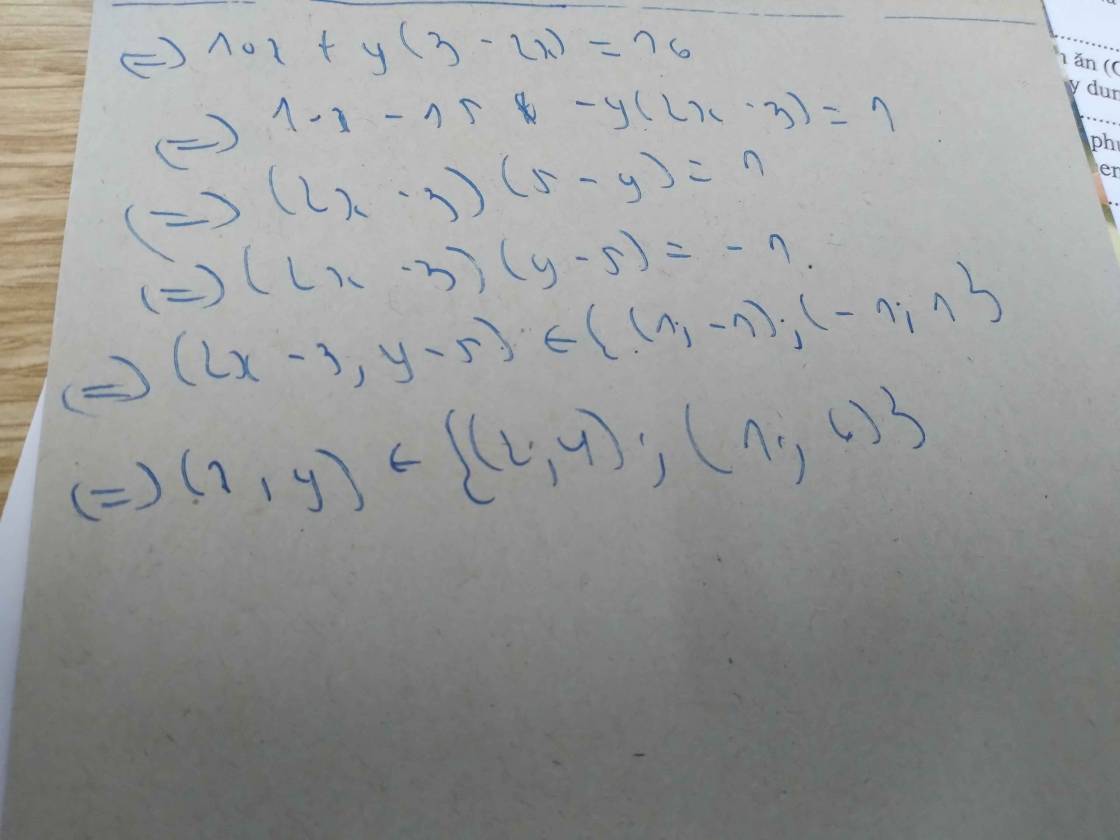
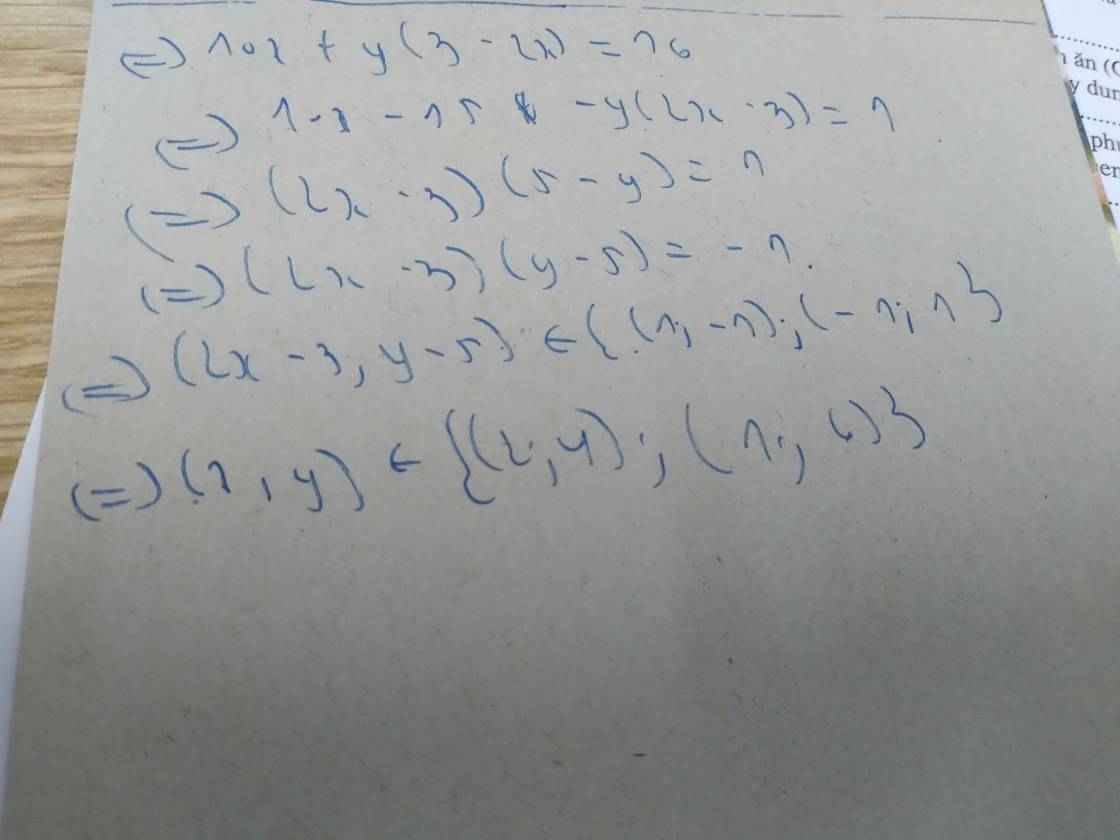
\(2xy+y=10x+17\Leftrightarrow y\left(2x+1\right)=10x+17\Leftrightarrow y=\frac{10x+17}{2x+1}.Vì,y,nguyên,nên:10x+17⋮2x+1\Leftrightarrow10x+5+12⋮2x+1\Leftrightarrow5\left(2x+1\right)+12⋮2x+1\Leftrightarrow12⋮2x+1.Mà,2x+1,lẻ,nên:2x+1\in\left\{-1;1;3;-3\right\}\Leftrightarrow2x\in\left\{-2;0;2;-4\right\}\Leftrightarrow x\in\left\{-1;0;1;-2\right\}\)
\(+,x=-1\Rightarrow-2y+y=7\Leftrightarrow-y=7\Leftrightarrow y=-7\Rightarrow\left(x,y\right)=\left(-1;-7\right)\left(thoaman\right)\)
\(+,x=0\Rightarrow y=17\left(thoaman\right)\)
\(+,x=1\Rightarrow3y=27\Rightarrow y=9\left(thoaman\right)\)
\(+,x=-2\Rightarrow-3y=-3\Leftrightarrow3y=3\Leftrightarrow y=1\left(thoaman\right)\)
\(Vậy:\left(x,y\right)\in\left\{\left(-1;-7\right);\left(0;17\right);\left(1;9\right);\left(-2;1\right)\right\}\)
\(2xy-10x+y=17\)
\(\Leftrightarrow2x\left(y-5\right)+\left(y-5\right)=12\)
\(\Leftrightarrow\left(2x+1\right)\left(y-5\right)=12\)
Vì x \(\in\) N nên 2x + 1 là ước lẻ của 12 \(\Rightarrow2x+1\in\left\{1;3\right\}\)
Ta có bảng sau: