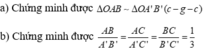Cho ΔOAB vuông tại, có OA = 6cm. Trên tia đối của tia OA lấy điểm A' sao cho OA'=\(\frac{1}{2}OA\). Từ A' vẽ đường thẳng vuông góc với AA' tại A', đường thẳng này cắt OB kéo dài tại B'. Tính OB và AB, biết A'B'=4,2cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TD
2 tháng 2 2022
Ta có :O là trung điểm của BC(gt)
O là trung điểm của AK(OA=OK)
=>ABKC là hình bình hành(dhnb)
Mà góc BAC = 90 độ
=>ABKC là hình chữ nhật (dhnb)
=>AB=CK và góc ACK = 90 độ
Xét tam giác ABC và tam giác CKA có:
AB=CK(cmt)
góc BAC=góc KCA( cùng bằng 90 độ)
AC chung
Vậy tam giác ABC = tam giác CKA(c.g.c)
b)Xét tam giác AHB và tam giác CHA có
góc AHB = góc CHA (=90 độ)
góc BAH =góc ACH(cùng phụ với góc B)
Vậy tam giác AHB đồng dạng tam giác CHA(g.g)
=>\(\dfrac{AB}{AH}=\dfrac{AC}{CH}\)(1)
Ta có AH\(\perp\)CH
ED\(\perp\)CH
=>AH//DE
Xét tam giác ACH có
AH//DE
=>\(\dfrac{AE}{HD}=\dfrac{AC}{CH}\)
=>\(\dfrac{AE}{AH}=\dfrac{AC}{CH}\)(do AH=AD)(2)
Từ(1) và (2) => \(\dfrac{AB}{AH}=\dfrac{AE}{AH}\)
=>AB=AE(đpcm)
3 tháng 1 2017
a) xét \(\Delta DOC,\Delta BOA:\)
\(\widehat{DOC}=\widehat{BOA}\left(đđ\right)\)
OA = OC ( gt )
OD = OB ( gt )
\(\rightarrow\Delta DOC=\Delta BOA\left(c.g.c\right)\)
\(\Rightarrow\widehat{ODC}=\widehat{OBA}\) ( 2 góc tương ứng )
mà chúng lại nằm ở vị trí so le trong
\(\Rightarrow\) AB// CD
c) xét \(\Delta IOM,\Delta FON:\)
ON = OM ( \(\Delta AOM=\Delta CON\) )
\(\widehat{O_1}=\widehat{O_2}\) ( đđ)
\(\widehat{I}=\widehat{F}=90^o\left(gt\right)\)
\(\rightarrow\Delta IOM=\Delta FON\) ( cạnh huyền góc nhọn )
\(\Rightarrow MI=NF\) ( 2 cạnh tương ứng )
CM
23 tháng 4 2018
Chỉ ra điểm O nằm giữa hai điểm A và B.
Tính được OB = 3 cm.
Vậy O là trung điểm của đoạn thẳng AB
T
25 tháng 8 2023
a) Ta thấy: M ∈ Ox; N ∈ Oy
Ox và Oy là 2 tia đối nhau
\(\Rightarrow\) Điểm O nằm giữa hai điểm M và N.
b) Vì M là trung điểm OA
\(\Rightarrow OM=AM=\dfrac{1}{2}\cdot OA\)
\(\Rightarrow OM=\dfrac{1}{2}\cdot6=3\left(cm\right)\) (do OA = 6cm)
Vì N là trung điểm OB
\(\Rightarrow ON=BN=\dfrac{1}{2}\cdot OB\)
\(\Rightarrow ON=\dfrac{1}{2}\cdot3=\dfrac{3}{2}\left(cm\right)\) (chỗ này sửa đề Oy = 3cm => OB = 3cm nhé)
Vì O ∈ MN \(\Rightarrow OM+ON=MN\)
\(\Rightarrow MN=3+\dfrac{3}{2}=4,5\left(cm\right)\)
